
分析 由于$\sqrt{18}$=3$\sqrt{2}$,且$\sqrt{x}$+$\sqrt{y}$=3$\sqrt{2}$,所以$\sqrt{x}$与$\sqrt{y}$是同类二次根式,又因为x,y都是正整数,所以$\sqrt{x}$=$\sqrt{3}$或2$\sqrt{3}$.
解答 解:∵$\sqrt{x}$+$\sqrt{y}$=3$\sqrt{2}$,
∴$\sqrt{x}$与$\sqrt{y}$是同类二次根式,
∵x与y是正整数,
∴$\sqrt{x}$=$\sqrt{2}$,$\sqrt{y}$=2$\sqrt{2}$或$\sqrt{x}$=2$\sqrt{2}$,$\sqrt{y}$=$\sqrt{2}$,
∴x=2,y=8或x=8,y=2,
∴x+y=10.
点评 本题考查二次根式的化简求知问题,涉及同类二次根式,分类讨论等知识,属于中等题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 值周老师调查各班的出缺勤学生情况 | |
| B. | 调查某种家具的顾客满意情况 | |
| C. | 调查某种钢笔的使用情况 | |
| D. | 了解夏季冷饮市场上冰淇淋的质量情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,∠ADE=46°,DF平分∠ADE,∠1=23°,求证:DF∥BE.
已知,如图,∠ADE=46°,DF平分∠ADE,∠1=23°,求证:DF∥BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
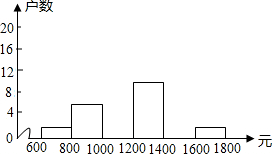 中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如图的频数分布表和频数分布直方图.
中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如图的频数分布表和频数分布直方图. | 分组 | 频数 | 百分比 |
| 600≤x<800 | 2 | 5% |
| 800≤x<1000 | 6 | 15% |
| 1000≤x<1200 | 45% | |
| 9 | 22.5% | |
| 1600≤x<1800 | 2 | |
| 合计 | 40 | 100% |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年湖北省枝江市九校七年级3月联考数学试卷(解析版) 题型:单选题
已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1 与∠2的关系一定成立的是( )
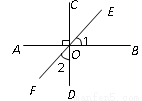
A. 相等 B. 互余 C. 互补 D. 互为对顶角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com