
某市区一条主要街道的改造工程有甲、乙两个工程队投标.经测算:若由两个工程队合做,12天恰好完成;若两个队合做9天后,剩下的由甲队单独完成,还需5天时间,现需从这两个工程队中选出一个队单独完成,从缩短工期角度考虑,你认为应该选择哪个队?为什么?


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
某景区内的环形路是边长为800米的正方形ABCD,如图1和图2.现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分.
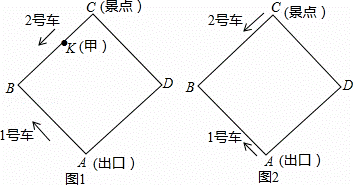
探究:设行驶吋间为t分.
(1)当0≤t≤8时,分别写出1号车、2号车在左半环线离出口A的路程y1,y2(米) 与t(分)的函数关系式,并求出当两车相距的路程是400米时t的值;
(2)t为何值时,1号车第三次恰好经过景点C?并直接写出这一段时间内它与2号车相遇过的次数.
发现:如图2,游客甲在BC上的一点K(不与点B,C重合)处候车,准备乘车到出口A,设CK=x米.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
比较哪种情况用时较多?(含候车时间)
决策:己知游客乙在DA上从D向出口A走去.步行的速度是50米/分.当行进到DA上一点P (不与点D,A重合)时,刚好与2号车迎面相遇.
(1)他发现,乘1号车会比乘2号车到出口A用时少,请你简要说明理由:
(2)设PA=s(0<s<800)米.若他想尽快到达出口A,根据s的大小,在等候乘1号车还是步行这两种方式中.他该如何选择?
查看答案和解析>>
科目:初中数学 来源: 题型:
关于反比例函数y= 的图象,下列说法正确的是( )
的图象,下列说法正确的是( )
A.图象经过点(1,1) B. 两个分支分布在第二、四象限
C.两个分支关于x轴成轴对称 D. 当x<0时,y随x的增大而减小


查看答案和解析>>
科目:初中数学 来源: 题型:
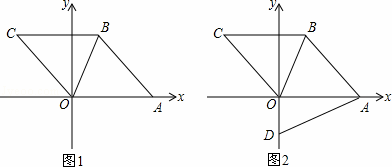
平面直角坐标系中,四边形ABCD是菱形,点C的坐标为(﹣3,4),点A在x轴的正半轴上,O为坐标原点,连接OB,抛物线y=ax2+bx+c经过C、O、A三点.
(1)直接写出这条抛物线的解析式;
(2)如图1,对于所求抛物线对称轴上的一点E,设△EBO的面积为S1,菱形ABCD的面积为S2,当S1≤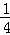 S2时,求点E的纵坐标n的取值范围;
S2时,求点E的纵坐标n的取值范围;
(3)如图2,D(0,﹣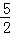 )为y轴上一点,连接AD,动点P从点O出发,以
)为y轴上一点,连接AD,动点P从点O出发,以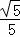 个单位/秒的速度沿OB方向运动,1秒后,动点Q从O出发,以2个单位/秒的速度沿折线O﹣A﹣B方向运动,设点P运动时间为t秒(0<t<6),是否存在实数t,使得以P、Q、B为顶点的三角形与△ADO相似?若存在,求出相应的t值;若不存在,请说明理由.
个单位/秒的速度沿OB方向运动,1秒后,动点Q从O出发,以2个单位/秒的速度沿折线O﹣A﹣B方向运动,设点P运动时间为t秒(0<t<6),是否存在实数t,使得以P、Q、B为顶点的三角形与△ADO相似?若存在,求出相应的t值;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图7,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)求证:△OAE ≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由.
(3)试求: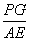 的值(结果保留根号).
的值(结果保留根号).
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
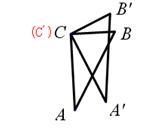
如图,两块完全相同的含30°角的直角三角板ABC和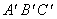 重合在一起,将三角板
重合在一起,将三角板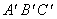 绕其顶点
绕其顶点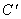 按逆时针方向旋转角α(0°< α≤90°),有以下四个结论:
按逆时针方向旋转角α(0°< α≤90°),有以下四个结论:
①当α=30°时,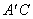 与
与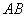 的交点恰好为
的交点恰好为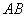 的中点;②当α=60°时,
的中点;②当α=60°时,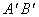 恰好经过点
恰好经过点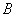 ;
;
③在旋转过程中,存在某一时刻,使得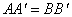 ; ④在旋转过程中,始终存在
; ④在旋转过程中,始终存在 ,其中结论正确的序号是 .(多填或填错得0分,少填酌情给分)
,其中结论正确的序号是 .(多填或填错得0分,少填酌情给分)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com