
·ÖÎö £¨1£©ÔʽÀ¨ºÅÖÐÁ½Ïîͨ·Ö²¢ÀûÓÃͬ·Öĸ·ÖʽµÄ¼Ó¼õ·¨Ôò¼ÆË㣬Լ·Ö¼´¿ÉµÃµ½½á¹û£»
£¨2£©ÔʽÀ¨ºÅÖÐÁ½Ïîͨ·Ö²¢ÀûÓÃͬ·Öĸ·ÖʽµÄ¼Ó¼õ·¨Ôò¼ÆË㣬ÀûÓóý·¨·¨Ôò±äÐΣ¬Ô¼·Ö¼´¿ÉµÃµ½½á¹û£»
£¨3£©ÔʽÀûÓóý·¨·¨Ôò±äÐΣ¬Ô¼·Ö¼´¿ÉµÃµ½½á¹û£®
½â´ð ½â£º£¨1£©Ôʽ=$\frac{£¨x-y£©^{2}+4xy}{x-y}$•$\frac{£¨x+y£©^{2}-4xy}{x+y}$=$\frac{£¨x+y£©^{2}£¨x-y£©^{2}}{£¨x+y£©£¨x-y£©}$=£¨x+y£©£¨x-y£©=x2-y2£»
£¨2£©Ôʽ=$\frac{{x}^{2}-{y}^{2}}{xy}$¡Â$\frac{{x}^{2}+{y}^{2}-2xy}{xy}$¡Â$\frac{x+y}{x}$=$\frac{£¨x+y£©£¨x-y£©}{xy}$•$\frac{xy}{£¨x-y£©^{2}}$•$\frac{x}{x+y}$=$\frac{x}{x-y}$£»
£¨3£©Ôʽ=$\frac{2£¨x+2y£©£¨x-2y£©}{-£¨2x-3y£©}$•$\frac{£¨2x-3y£©^{2}}{x£¨x-2y£©}$=-$\frac{2£¨x+2y£©£¨2x-3y£©}{x}$£®
µãÆÀ ´ËÌ⿼²éÁË·ÖʽµÄ»ìºÏÔËË㣬ÊìÁ·ÕÆÎÕÔËËã·¨ÔòÊǽⱾÌâµÄ¹Ø¼ü£®


 ÃûУ¿ÎÌÃϵÁдð°¸
ÃûУ¿ÎÌÃϵÁдð°¸
| Ä꼶 | ¸ßÖÐ¿Î³Ì | Ä꼶 | ³õÖÐ¿Î³Ì |
| ¸ßÒ» | ¸ßÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ß¶þ | ¸ß¶þÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ßÈý | ¸ßÈýÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍƼö£¡ |
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
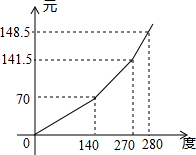 Î人ÊÐ2012Äê4Ô¾ÓÃñÓõç×¼±¸ÊµÐн×Ìݵç¼Û£¬µÚÒ»µµÎª140¡ãÒÔÄÚ¼Û¸ñ²»±ä£¬µÚ¶þµµÎª140¡ã-270¡ã¼Û¸ñ΢µ÷£¬µÚÈýµµ³¬¹ý270¡ãÒÔÉϼ۸ñÔÙ¼ÓÒ»µã£¬Ã¿¸öÔµĵç·Ñy£¨Ôª£©ÓëÓõçÁ¿x£¨¶È£©µÄº¯Êý¹ØϵÈçͼËùʾ£¬Èôij¾ÓÃñ9Ô·ÝÓõç300¶È£¬µç·Ñµ÷Õûºó½«¶àÖ§³ö12.5Ôª£®
Î人ÊÐ2012Äê4Ô¾ÓÃñÓõç×¼±¸ÊµÐн×Ìݵç¼Û£¬µÚÒ»µµÎª140¡ãÒÔÄÚ¼Û¸ñ²»±ä£¬µÚ¶þµµÎª140¡ã-270¡ã¼Û¸ñ΢µ÷£¬µÚÈýµµ³¬¹ý270¡ãÒÔÉϼ۸ñÔÙ¼ÓÒ»µã£¬Ã¿¸öÔµĵç·Ñy£¨Ôª£©ÓëÓõçÁ¿x£¨¶È£©µÄº¯Êý¹ØϵÈçͼËùʾ£¬Èôij¾ÓÃñ9Ô·ÝÓõç300¶È£¬µç·Ñµ÷Õûºó½«¶àÖ§³ö12.5Ôª£®²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
| Éä»÷´ÎÊýn | 10 | 20 | 50 | 100 | 200 | 500 |
| »÷ÖаÐÐÄ´ÎÊým | 9 | 19 | 44 | 91 | 178 | 450 |
| »÷ÖаÐÐÄƵÂÊ$\frac{m}{n}$ |
²é¿´´ð°¸ºÍ½âÎö>>
°Ù¶ÈÖÂÐÅ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨Æ½Ì¨ | ÍøÉÏÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | µçÐÅթƾٱ¨×¨Çø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com