
分析 a1,a2,a3,…an为彼此两两不等的非负整数,即是不重复的非负整数,2的10次方为1024,11次方为2048,所以这几个数在0~10之间.全部相加1+2+4+8+16+32+64+128+256+512+1024=2047,多了46,观察可得是2+4+8+32=46,所以那几个数是:0、4、6、7、8、9、10,和为44.
解答 解:∵2的10次方为1024,11次方为2048,
∴a1,a2,a3,…an几个数在0~10之间,
∵20+21+22+23+…+210,
=1+2+4+8+16+32+64+128+256+512+1024=2047,
2047-2001=46,
2+4+8+32=46,即21+22+23+25=46,
则a1+a2+a3+…+an=0+4+6+7+8+9+10=44,
故答案为:44.
点评 本题是数字类的规律题,有难度;首先理解指数为不重复的非负整数,其次是计算2的指数幂的结果,与和2001的关系,利用排除法得出结论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
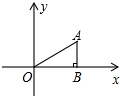 如图,在平面直角坐标系xOy中,点B在x轴的正半轴上,OB=$\sqrt{3}$,AB⊥OB,∠AOB=30°.把△ABO绕点O逆时针旋转150°后得到△A1B1O,则点A的对应点A1的坐标为( )
如图,在平面直角坐标系xOy中,点B在x轴的正半轴上,OB=$\sqrt{3}$,AB⊥OB,∠AOB=30°.把△ABO绕点O逆时针旋转150°后得到△A1B1O,则点A的对应点A1的坐标为( )| A. | (0,-2) | B. | (-2,0) | C. | (-1,$-\sqrt{3}$) | D. | ($-\sqrt{3}$,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2)2>-32 | B. | -0.3<-$\frac{1}{3}$ | C. | -$\frac{4}{5}$<-$\frac{7}{6}$ | D. | -$\frac{10}{9}$>-$\frac{9}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com