
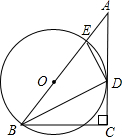
 (2012•朝阳二模)已知:如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,DE⊥DB交AB于点E.
(2012•朝阳二模)已知:如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,DE⊥DB交AB于点E.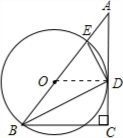
| AC2+BC2 |
| AO |
| AB |
| OD |
| BC |
| 15-r |
| 15 |
| r |
| 9 |
| 45 |
| 8 |


科目:初中数学 来源: 题型:
 (2012•朝阳二模)如图,抛物线y=
(2012•朝阳二模)如图,抛物线y=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•朝阳二模)为了深化课堂教学改革,促进学生全面发展,某校积极进行课改实验.学校为了鼓励其中表现突出的同学,每学月进行“校园之星”评选活动.初2012级对本年级上学期五个学月的获奖人数进行了统计,并制成了如下不完整的折线统计图.
(2012•朝阳二模)为了深化课堂教学改革,促进学生全面发展,某校积极进行课改实验.学校为了鼓励其中表现突出的同学,每学月进行“校园之星”评选活动.初2012级对本年级上学期五个学月的获奖人数进行了统计,并制成了如下不完整的折线统计图.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com