
 ,AC=BC,CD⊥AB于点D,点E为AC边上一点,联结BE交CD于点F,过点E作EG⊥BE交AB于点G,
,AC=BC,CD⊥AB于点D,点E为AC边上一点,联结BE交CD于点F,过点E作EG⊥BE交AB于点G,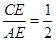 ,探究线段EF与EG的数量关系并且证明;
,探究线段EF与EG的数量关系并且证明;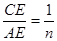 ,线段EF与EG的数量关系是 .
,线段EF与EG的数量关系是 .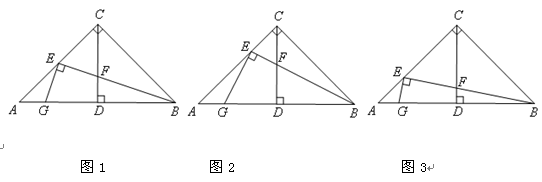
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源:不详 题型:解答题
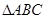 和
和 是绕点
是绕点 旋转的两个相似三角形,其中
旋转的两个相似三角形,其中 与
与 、
、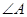 与
与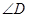 为对应角.
为对应角.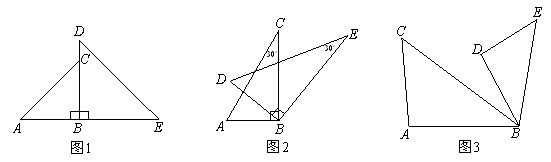
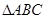 和
和 分别是以
分别是以 与
与 为顶角的等腰直角三角形,且两三角形旋转到使点
为顶角的等腰直角三角形,且两三角形旋转到使点 、
、 、
、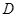 在同一条直线上的位置时,请直接写出线段
在同一条直线上的位置时,请直接写出线段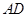 与线段
与线段 的关系;
的关系;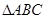 和
和 为含有
为含有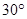 角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段
角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段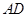 与线段
与线段 的关系,并说明理由;
的关系,并说明理由;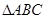 和
和 为如图3的两个三角形,且
为如图3的两个三角形,且 =
= ,
,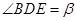 ,在绕点
,在绕点 旋转的过程中,直线
旋转的过程中,直线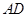 与
与 夹角的度数是否改变?若不改变,直接用含
夹角的度数是否改变?若不改变,直接用含 、
、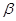 的式子表示夹角的度数;若改变,请说明理由.
的式子表示夹角的度数;若改变,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
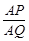 的值等于 ▲
的值等于 ▲ 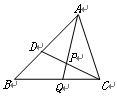
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
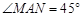 ,连结MC,NC,MN.
,连结MC,NC,MN.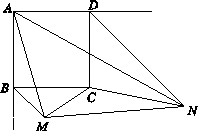
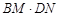 = ;(用含a的代数式表示)
= ;(用含a的代数式表示)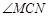 的度数;
的度数;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 =
= ;③AC?BE=12;④3BF=4AC.其中结论正确的个数有( )
;③AC?BE=12;④3BF=4AC.其中结论正确的个数有( )
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 =BF.
=BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com