
分析 (1)先根据一元二次方程根与系数的关系确定出x1与x2的两根之积与两根之和的值,代入所求的代数式即可得到结果;
(2)先根据一元二次方程根与系数的关系确定出x1与x2的两根之积与两根之和的值,代入所求的代数式即可得到结果;
解答 解:根据题意得:x1+x2=-$\frac{12}{6}$=-2,x1•x2=$\frac{-9}{6}$=-$\frac{3}{2}$,
(1)|x1-x2|=$\sqrt{{{(x}_{1}{-x}_{2})}^{2}}$=$\sqrt{{{(x}_{1}{+x}_{2})}^{2}-{4x}_{1}{•x}_{2}}$=$\sqrt{{(-2)}^{2}-4×(-\frac{3}{2})}$=$\sqrt{10}$,
(2)x13+x23.=(x1+x2)[${{(x}_{1}{+x}_{2})}^{2}$-3x1•x2]=-17.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-$\frac{b}{a}$x1•x2=$\frac{c}{a}$.也考查了代数式的变形能力.


科目:初中数学 来源: 题型:解答题
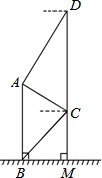 在数学活动课上,为测量教学楼前的一座雕塑AB的高度.小明在二楼C处,利用测角仪测得雕塑顶端A处的仰角为30°,底部B处的俯角为45°,小华在五楼D处,利用测角仪测得雕塑顶端A处的俯角为60°.若CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).
在数学活动课上,为测量教学楼前的一座雕塑AB的高度.小明在二楼C处,利用测角仪测得雕塑顶端A处的仰角为30°,底部B处的俯角为45°,小华在五楼D处,利用测角仪测得雕塑顶端A处的俯角为60°.若CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com