某开发公司生产了若干件某种新产品需要精加工后才能投放市场,现有甲、乙两个加工厂都想加工这批产品.已知甲、乙两个工厂每天分别能加工这种产品16件和24件,且知单独加工这批产品甲厂比乙厂要多用20天.又知若由甲厂单独做,公司需付甲厂每天费用80元;若由乙厂单独做,公司需付乙厂每天费用120元.
(1)求这批新产品共有多少件?
(2)若公司董事会制定了如下方案:可以由每个厂家单独完成;也可以由两个厂家同时合作完成,但在加工过程中,公司需派一名工程师到厂进行技术指导,并由公司为其提供每天5元的午餐补助费,请你帮助公司选择一种既省时又省钱的加工方案,并通过计算说明理由.
解:(1)设这个公司要加工x件新产品,由题意得:
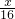
-
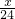
=20,
解得:x=960(件),
答:这个公司要加工960件新产品;
(2)①由甲厂单独加工:需要耗时为
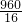
=60天,需要费用为:60×(5+80)=5100元;
②由乙厂单独加工:需要耗时为
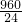
=40天,需要费用为:40×(120+5)=5000元;
③由两场厂共同加工:需要耗时为

=24天,需要费用为:24×(80+120+5)=4920元.
所以,由两厂合作同时完成时,即省钱,又省时间.
分析:(1)设这个公司要加工x件新产品,则可知甲厂需
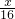
天,乙厂需要
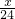
天,单独加工这批产品甲厂比乙厂要多用20天,根据题意找出等量关系,根据此等量关系列出方程求解即可.
(2)应分为三种情况讨论:①由甲厂单独加工;②由乙厂单独加工;③由两场厂共同加工,分别比较三种情况下,所耗时间和花费金额,求出即省钱,又省时间的加工方案.
点评:本题主要考查一元一次方程的应用,关键在于理解清楚题意,找出等量关系列出方程.对于要求最符合要求类型的题目,应将所有方案,列出来求出符合题意的那一个即可.

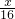 -
-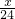 =20,
=20,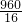 =60天,需要费用为:60×(5+80)=5100元;
=60天,需要费用为:60×(5+80)=5100元;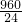 =40天,需要费用为:40×(120+5)=5000元;
=40天,需要费用为:40×(120+5)=5000元; =24天,需要费用为:24×(80+120+5)=4920元.
=24天,需要费用为:24×(80+120+5)=4920元.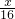 天,乙厂需要
天,乙厂需要 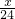 天,单独加工这批产品甲厂比乙厂要多用20天,根据题意找出等量关系,根据此等量关系列出方程求解即可.
天,单独加工这批产品甲厂比乙厂要多用20天,根据题意找出等量关系,根据此等量关系列出方程求解即可.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案