
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源:不详 题型:解答题
 在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 内,画出使
内,画出使 的一个点
的一个点 ,并说明理由.
,并说明理由. 内(含边),画出使
内(含边),画出使 的所有的点
的所有的点 ,并说明理由.
,并说明理由. .工人师傅想用它裁出两块全等的、面积最大的
.工人师傅想用它裁出两块全等的、面积最大的 和
和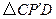 钢板,且
钢板,且 .请你在图③中画出符合要求的点
.请你在图③中画出符合要求的点 和
和 ,并求出
,并求出 的面积(结果保留根号).
的面积(结果保留根号).
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com