
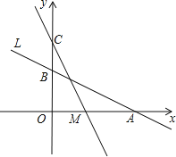
【题目】如图,直线L:![]() 与x轴、y轴分别交于A、B两点,在y轴上有一点
与x轴、y轴分别交于A、B两点,在y轴上有一点![]() ,动点M从A点以每秒1个单位的速度沿x轴向左移动.
,动点M从A点以每秒1个单位的速度沿x轴向左移动.
![]() 求A、B两点的坐标;
求A、B两点的坐标;
![]() 求
求![]() 的面积S与M的移动时间t之间的函数关系式;
的面积S与M的移动时间t之间的函数关系式;
![]() 当t为何值时
当t为何值时![]() ≌
≌![]() ,并求此时M点的坐标.
,并求此时M点的坐标.
【答案】(1)A(0,4),B(0,2);(2)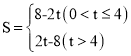 ;(3)当t=2或6时,△COM≌△AOB,此时M(2,0)或(﹣2,0).
;(3)当t=2或6时,△COM≌△AOB,此时M(2,0)或(﹣2,0).
【解析】
(1)由直线L的函数解析式,令y=0求A点坐标,x=0求B点坐标;
(2)由面积公式S=![]() OMOC求出S与t之间的函数关系式;
OMOC求出S与t之间的函数关系式;
(3)若△COM≌△AOB,OM=OB,则t时间内移动了AM,可算出t值,并得到M点坐标.
(1)∵y=﹣![]() x+2,
x+2,
当x=0时,y=2;当y=0时,x=4,
则A、B两点的坐标分别为A(4,0)、B(0,2);
(2)∵C(0,4),A(4,0)
∴OC=OA=4,
当0≤t≤4时,OM=OA﹣AM=4﹣t,S△OCM=![]() ×4×(4﹣t)=8﹣2t;
×4×(4﹣t)=8﹣2t;
当t>4时,OM=AM﹣OA=t﹣4,S△OCM=![]() ×4×(t﹣4)=2t﹣8;
×4×(t﹣4)=2t﹣8;
∴![]() 的面积S与M的移动时间t之间的函数关系式为:
的面积S与M的移动时间t之间的函数关系式为: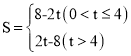
(3)∵OC=OA,∠AOB=∠COM=90°,
∴只需OB=OM,则△COM≌△AOB,
即OM=2,
此时,若M在x轴的正半轴时,t=2,
M在x轴的负半轴,则t=6.
故当t=2或6时,△COM≌△AOB,此时M(2,0)或(﹣2,0).


科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为66万元;本周已售出2辆A型车和1辆B型车,销售额为42万元.
(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不超过84万元.问最多可以购买多少辆B型号的新能源汽车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
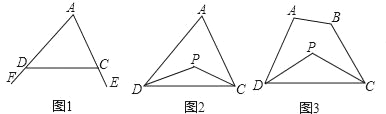
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校创新能力大赛的笔试情况,随机抽查了部分参赛同学的成绩,整理并制作了如下统计表和统计图(不完整) ,请根据图表中提供的信息解答问题:
得分 | 频数 | 百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(1)本次调查的总人数为_______人;
(2)在统计表中,![]() =____,
=____,![]() =__;在扇形统计图中“
=__;在扇形统计图中“![]() ”所在扇形的圆心角的度数为_______
”所在扇形的圆心角的度数为_______
(3)补全频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现:若每箱以50元的价格出售,平均每天销售80箱,价格每提高1元,平均每天少销售2箱.
⑴.求平均每天销售量![]() (箱)与销售价
(箱)与销售价![]() (元/箱)之间的函数关系式;
(元/箱)之间的函数关系式;
⑵.求该批发商平均每天的销售利润![]() (元)与销售价
(元)与销售价![]() (元/箱)之间的函数关系式;
(元/箱)之间的函数关系式;
⑶.当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解读基础:
(1)图1形似燕尾,我们称之为“燕尾形”,请写出![]() 、
、![]() 、
、![]() 、
、![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
(2)图2形似8字,我们称之为“八字形”,请写出![]() 、
、![]() 、
、![]() 、
、![]() 之间的关系,并说明理由:
之间的关系,并说明理由:
应用乐园:直接运用上述两个结论解答下列各题
(3)①如图3,在![]() 中,
中,![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,请直接写出
,请直接写出![]() 和
和![]() 的关系 ;
的关系 ;
②如图4,![]() .
.
(4)如图5,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,
,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,已知
,已知![]() ,
,![]() ,求
,求![]() 和
和![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)绘制相应的频数分布折线图.
(4)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com