

分析 (1)由四边形EFGH是正方形,根据正方形的对角线相等且互相平分可得CF=CE=x,根据BE=$\frac{1}{2}$-x,由三角形的面积公式即可得出S△ABE=$\frac{1}{2}$AB•BE=$\frac{1}{2}$×$\frac{1}{2}$×($\frac{1}{2}$-x);
(2)先根据S四边形AEFD=S正方形ABCD-S△CFE-S△ABE,求出S四边形AEFD=-$\frac{1}{2}$x2+$\frac{1}{4}$x+$\frac{1}{8}$,再由每块地砖的成本价为4元列出关于x的一元二次方程,求出即可.
解答 解:(1)CF=x,
S△ABE=$\frac{1}{2}$AB•BE=$\frac{1}{2}$×$\frac{1}{2}$×($\frac{1}{2}$-x)=$\frac{1}{8}$-$\frac{1}{4}$x.
故答案为x,$\frac{1}{8}$-$\frac{1}{4}$x; (2)∵CE=x,则BE=$\frac{1}{2}$-x,CF=CE=x,
(2)∵CE=x,则BE=$\frac{1}{2}$-x,CF=CE=x,
∵S△CFE=$\frac{1}{2}$x2,S△ABE=$\frac{1}{8}$-$\frac{1}{4}$x,
∴S四边形AEFD=S正方形ABCD-S△CFE-S△ABE
=($\frac{1}{2}$)2-$\frac{1}{2}$x2-($\frac{1}{8}$-$\frac{1}{4}$x)
=$\frac{1}{4}$-$\frac{1}{2}$x2-$\frac{1}{8}$+$\frac{1}{4}$x=-$\frac{1}{2}$x2+$\frac{1}{4}$x+$\frac{1}{8}$,
由题意得:
30×$\frac{1}{2}$x2+20×($\frac{1}{8}$-$\frac{1}{4}$x)+10×(-$\frac{1}{2}$x2+$\frac{1}{4}$x+$\frac{1}{8}$)+0.35=4,
化简得:10x2-2.5x+0.1=0,
b2-4ac=6.25-4=2.25,
∴x=$\frac{2.5±1.5}{2×10}$,
∴x1=0.2,x2=0.05(不合题意舍去).
答:CE的长应为0.2m.
点评 此题主要考查了一元二次方程的应用以及图形面积求法等知识,借助数形结合得出图形面积关系是解题关键.


科目:初中数学 来源: 题型:填空题
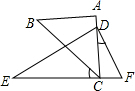 将一副直角三角尺如图摆放,点C在EF上,AC经过点D,已知∠A=∠EDF=90°,∠B=45°,∠E=30°,∠BCE=40°,则∠CDF的度数为25°.
将一副直角三角尺如图摆放,点C在EF上,AC经过点D,已知∠A=∠EDF=90°,∠B=45°,∠E=30°,∠BCE=40°,则∠CDF的度数为25°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,按要求解答下列问题:
如图所示,按要求解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示.把三角板和刻度尺的直角顶点重合放置,则下列结论:①∠1=30°;②∠1=∠3;③∠1+∠3=∠2;④把三角板绕点A旋转适当的角度,可使∠1=∠2=∠3成立,则上述结论中,你认为一定正确的结论有②④(只需填上相应结论的顺序号即可).
如图所示.把三角板和刻度尺的直角顶点重合放置,则下列结论:①∠1=30°;②∠1=∠3;③∠1+∠3=∠2;④把三角板绕点A旋转适当的角度,可使∠1=∠2=∠3成立,则上述结论中,你认为一定正确的结论有②④(只需填上相应结论的顺序号即可).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com