
【题目】一个多项式加上5x2+3x-2的2倍得1-3x2+x , 求这个多项式
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<![]() ).
).

(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)在运动过程中,当直线MN与⊙O相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门. ![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a、b满足|a+3|+(b+3a)2=0. ![]()
(1)求点C表示的数;
(2)点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动,若AP+BQ=2PQ,求时间t;
(3)若点P从A向右运动,点M为AP中点,在P点到达点B之前:① ![]() 的值不变;②2BM﹣BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.
的值不变;②2BM﹣BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,a、b、c在数轴上的位置如图. ![]()
(1)填空:a、b之间的距离为;b、c之间的距离为;a、c之间的距离为 .
(2)化简:|a+1|﹣|c﹣b|+|b﹣1|.
(3)若a+b+c=0,且b与﹣1的距离和c与﹣1的距离相等,求﹣a2+2b﹣c﹣(a﹣4c﹣b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
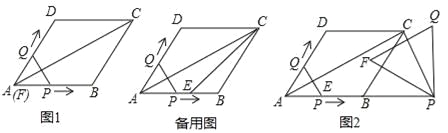
【题目】已知:如图1,菱形ABCD的边长为6,∠DAB=60°,点E是AB的中点,连接AC、EC.点Q从点A出发,沿折线A﹣D﹣C运动,同时点P从点A出发,沿射线AB运动,P、Q的速度均为每秒1个单位长度;以PQ为边在PQ的左侧作等边△PQF,△PQF与△AEC重叠部分的面积为S,当点Q运动到点C时P、Q同时停止运动,设运动的时间为t.
(1)当等边△PQF的边PQ恰好经过点D时,求运动时间t的值;当等边△PQF的边QF 恰好经过点E时,求运动时间t的值;
(2)在整个运动过程中,请求出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)如图2,当点Q到达C点时,将等边△PQF绕点P旋转α°(0<α<360),直线PF分别与直线AC、直线CD交于点M、N.是否存在这样的α,使△CMN为等腰三角形?若存在,请直接写出此时线段CM的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店将进货价为20元/盒的百合花,在市场参考价28~38元的范围内定价36元/盒销售,这样平均每天可售出40盒,经过市场调查发现,在进货价不变的情况下,若每盒下调1元,则平均每天可多销售10盒,要使每天的利润达到750元,应将每盒百合花在售价上下调多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com