
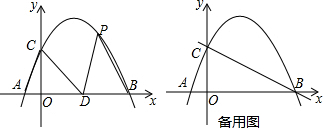
���� ��1������������y=ax2+bx+2������A��-1��0���͵�B��4��0����Ӧ�ô���ϵ����������������ߵĽ���ʽ���ɣ�
��2�����ȸ��������ε�������������CAD����������������PDB�������Ȼ�����BD=2���������|n|=3���ݴ��жϳ�n=3��-3���ٰ������������ߵĽ���ʽ�����x��ֵ�Ƕ��٣������жϳ���P�����꣮
��3������Ӧ�ô���ϵ���������BC���ڵ�ֱ�ߵĽ���ʽ�Ƕ��٣�Ȼ����ݵ�P�������ǣ�m��n���������F�����꣬�ٸ��ݶ��κ�����ֵ�������EG2����Сֵ�Ƕ��٣���������߶�EG����Сֵ��
��� �⣺��1����A��-1��0����B��4��0��������������y=ax2+bx+2�У��ɵ�
$\left\{\begin{array}{l}{a-b+2=0}\\{16a+4b+2=0}\end{array}\right.$
���$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$
�������ߵĽ���ʽΪ��y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
��2���������ߵĽ���ʽΪy=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
���C�������ǣ�0��2����
�ߵ�A��-1��0������D��2��0����
��AD=2-��-1��=3��
���CAD�����=$\frac{1}{2}��3��2=3$��
���PDB�����=3��
�ߵ�B��4��0������D��2��0����
��BD=2��
��|n|=3��2��2=3��
��n=3��-3��
�ٵ�n=3ʱ��
-$\frac{1}{2}$m2+$\frac{3}{2}$m+2=3��
���m=1��m=2��
���P�������ǣ�1��3����2��3����
�ڵ�n=-3ʱ��
-$\frac{1}{2}$m2+$\frac{3}{2}$m+2=-3��
���m=5��m=-2��
���P�������ǣ�5��-3����-2��-3����
���ϣ��ɵ�
��P�������ǣ�1��3������2��3������5��-3����-2��-3����
��3����ͼ1��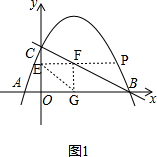
��BC���ڵ�ֱ�ߵĽ���ʽ�ǣ�y=mx+n��
�ߵ�C�������ǣ�0��2������B�������ǣ�4��0����
��$\left\{\begin{array}{l}{n=2}\\{4m+n=0}\end{array}\right.$
���$\left\{\begin{array}{l}{m=-\frac{1}{2}}\\{n=2}\end{array}\right.$
��BC���ڵ�ֱ�ߵĽ���ʽ�ǣ�y=-$\frac{1}{2}$x+2��
�ߵ�P�������ǣ�m��n����
���F�������ǣ�4-2n��n����
��EG2=��4-2n��2+n2=5n2-16n+16=5��n-$\frac{8}{5}$��2+$\frac{16}{5}$��
��n��0��
�൱n=$\frac{8}{5}$ʱ���߶�EG����Сֵ�ǣ�$\sqrt{\frac{16}{5}}=\frac{4}{5}\sqrt{5}$��
���߶�EG����Сֵ��$\frac{4}{5}\sqrt{5}$��
���� ��1��������Ҫ�����˶��κ����ۺ��⣬�����˷������������������˷�������˼���Ӧ�ã����������ν��˼���Ӧ�ã������˴���֪����ͼ���л�ȡ��Ϣ���������û�ȡ����Ϣ�����Ӧ�������������
��2����������˴���ϵ������ֱ�ߡ���������ʽ�ķ�����Ҫ�������գ�
��3����������������ε��������Ҫ�������գ�


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 2 | C�� | -3 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��A��C��?BFDE�ĶԽ���EF���ڵ�ֱ���ϣ���AE=CF����֤��BC��AD��
��ͼ��A��C��?BFDE�ĶԽ���EF���ڵ�ֱ���ϣ���AE=CF����֤��BC��AD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 13 | B�� | 12 | C�� | 11 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪���κ���y=ax2+bx+2������ͼ���㣨1��2����
��֪���κ���y=ax2+bx+2������ͼ���㣨1��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
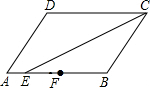 ��ͼ����?ABCD�У�CEƽ�֡�DCB��F��AB���е㣬AB=8��BC=6����AE��EF��FB=1��1��2��
��ͼ����?ABCD�У�CEƽ�֡�DCB��F��AB���е㣬AB=8��BC=6����AE��EF��FB=1��1��2���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com