
 已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,BE=DF.
已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,BE=DF.分析 (1)利用正方形的性质可证明△ABE≌△ADF,可得AE=AF;
(2)首先证明四边形AEMF是平行四边形,再证明AE=AF即可;
解答 解:(1)∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
∵BE=DF,
∴Rt△ABE≌Rt△ADF,
∴AE=AF.
(2)四边形AEMF是菱形.
理由:∵四边形ABCD是正方形,
∴∠BCA=∠DCA=45°,
BC=DC(正方形邻边相等),
∵BE=DF,
∴BC-BE=DC-DF(等式的性质),
即CE=CF,
∴OE=OF,
∵OM=OA,
∴四边形AEMF是平行四边形,
∵AE=AF,
∴平行四边形AEMF是菱形.
点评 本题考查正方形的性质、菱形的判定、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:填空题
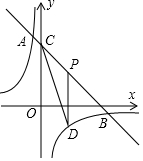 如图,直线y=-x+8与双曲线y=$\frac{k}{x}$相交于A,B两点,与y轴交于点C,点P是线段BC上的动点(点P不与点B,C重合),过P作y轴的平行线,交双曲线于点D,连接CD,若点A的横坐标为-1,则△PDC的面积的最大值为$\frac{25}{2}$.
如图,直线y=-x+8与双曲线y=$\frac{k}{x}$相交于A,B两点,与y轴交于点C,点P是线段BC上的动点(点P不与点B,C重合),过P作y轴的平行线,交双曲线于点D,连接CD,若点A的横坐标为-1,则△PDC的面积的最大值为$\frac{25}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2×103 | B. | 2×104 | C. | 20×103 | D. | 0.2×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>0 | B. | a<0 | C. | a>-$\frac{1}{2}$ | D. | a<-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>$\frac{4}{5}$ | B. | x≥8 | C. | $\frac{4}{5}$<x≤8 | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.
我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 型号 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 数量(双) | 2 | 6 | 11 | 15 | 7 | 3 | 4 |
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,不等式ax+b>$\frac{k}{x}$的解集为( )
已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,不等式ax+b>$\frac{k}{x}$的解集为( )| A. | x<-3 | B. | x<-3或x>1 | C. | -3<x<0或x>1 | D. | -3<x<1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com