
分析 (1)要求m的取值范围也要先求出x,y的值,然后由给出的x为正数即>0,列出不等式方程组,再解不等式方程即可;
(2)和(1)同理,只不过满足的条件不同.
解答 解:$\left\{\begin{array}{l}{3x-1=-y,①}\\{x-m=2y,②}\end{array}\right.$
①×2+②得7x=2+m
解得x=$\frac{2+m}{7}$,
把x=$\frac{2+m}{7}$代入①得y=$\frac{1-3m}{7}$.
(1)若方程组的解满足x为正数
即$\frac{2+m}{7}$>0解得m>-2;
(2)若方程组的解满足x>y
即$\frac{2+m}{7}$>$\frac{1-3m}{7}$,
解得m>-$\frac{1}{4}$.
点评 此题的关键是先求出x,y的值再按要求列不等式,解不等式.注意解不等式时不等号的变化.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:选择题
| A. | x1=3,x2=-3 | B. | x1=x2=0 | C. | x1=$\sqrt{6}$,x2=-$\sqrt{6}$ | D. | x1=3$\sqrt{2}$,x2=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
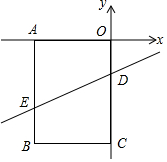 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(-2,-3),直线y=$\frac{1}{2}$x-1与OC、AB分别交于占D、E,点P在矩形的边AB或BC上,作PF⊥ED于点F,连接PD,当△PFD是等腰三角形时,点P的坐标为(-$\frac{2}{3}$,-3)或(-2,-$\frac{1}{3}$).
如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(-2,-3),直线y=$\frac{1}{2}$x-1与OC、AB分别交于占D、E,点P在矩形的边AB或BC上,作PF⊥ED于点F,连接PD,当△PFD是等腰三角形时,点P的坐标为(-$\frac{2}{3}$,-3)或(-2,-$\frac{1}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
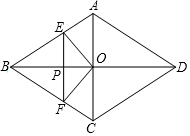 如图,菱形ABCD的对角线AC与BD交于点O,AC=6,BD=8.动点E从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止.点F是点E关于BD的对称点,EF交BD于点P,若BP=x,△OEF的面积为y,则y与x之间的函数图象大致为( )
如图,菱形ABCD的对角线AC与BD交于点O,AC=6,BD=8.动点E从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止.点F是点E关于BD的对称点,EF交BD于点P,若BP=x,△OEF的面积为y,则y与x之间的函数图象大致为( )| A. | 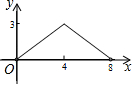 | B. | 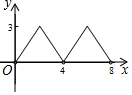 | C. | 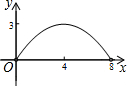 | D. | 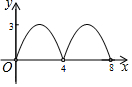 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com