练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如果＝36，求x

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    三角形中，顶角等于36°的等腰三角形称为黄金三角形，如图1，在△ABC中，已知：AB＝AC，且∠A＝36°．

     

     

      1.在图1中，用尺规作AB的垂直平分线交AC于D，并连接BD（保留作图痕迹，不写作法）；

       2.△BCD是不是黄金三角形，如果是，请给出证明；如果不是，请说明理由；

       3.设，试求k的值；

      4.如图2，在△A1B1C1中，已知A1B1＝A1C1，∠A1＝108°，且A1B1＝AB，

    请直接写出的值．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年安徽省马鞍山六中中考模拟数学卷 题型：解答题

    三角形中，顶角等于36°的等腰三角形称为黄金三角形，如图1，在△ABC中，已知：AB＝AC，且∠A＝36°．

    【小题1】在图1中，用尺规作AB的垂直平分线交AC于D，并连接BD（保留作图痕迹，不写作法）；
    【小题2】△BCD是不是黄金三角形，如果是，请给出证明；如果不是，请说明理由；
    【小题3】设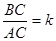，试求k的值；
    【小题4】如图2，在△A1B1C1中，已知A1B1＝A1C1，∠A1＝108°，且A1B1＝AB，
    请直接写出的值．

    查看答案和解析>>

    科目：初中数学 来源：2013届江苏省南京市白下区中考二模数学试卷（带解析） 题型：解答题

    （1）如图①，P为△ABC的边AB上一点（P不与点A、点B重合），连接PC，如果△CBP∽△ABC，那么就称P为△ABC的边AB上的相似点．
    画法初探
    ①如图②，在△ABC中，∠ACB＞90°，画出△ABC的边AB上的相似点P（画图工具不限，保留画图痕迹或有必要的说明）；

    辩证思考
    ②是不是所有的三角形都存在它的边上的相似点？如果是，请说明理由；如果不是，请找出一个不存在边上相似点的三角形；
    特例分析
    ③已知P为△ABC的边AB上的相似点，连接PC，若△ACP∽△ABC，则△ABC的形状是   ；
    ④如图③，在△ABC中，AB＝AC，∠A＝36°，P是边AB上的相似点，求的值．
    （2）在矩形ABCD中，AB＝a，BC＝b（a≥b）．P是AB上的点（P不与点A、点B重合），作PQ⊥CD，垂足为Q．如果矩形ADQP∽矩形ABCD，那么就称PQ为矩形ABCD的边AB、CD上的相似线．

    ①类比（1）中的“画法初探”，可以提出问题：对于如图④的矩形ABCD，在不限制画图工具的前提下，如何画出它的边AB、CD上的相似线PQ呢？
    你的解答是：   （只需描述PQ的画法，不需在图上画出PQ）．
    ②请继续类比（1）中的“辩证思考”、“特例分析”两个栏目对矩形的相似线进行研究，要求每个栏目提出一个问题并解决．

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年江苏省南京市白下区中考二模数学试卷（解析版） 题型：解答题

    （1）如图①，P为△ABC的边AB上一点（P不与点A、点B重合），连接PC，如果△CBP∽△ABC，那么就称P为△ABC的边AB上的相似点．

    画法初探

    ①如图②，在△ABC中，∠ACB＞90°，画出△ABC的边AB上的相似点P（画图工具不限，保留画图痕迹或有必要的说明）；

    辩证思考

    ②是不是所有的三角形都存在它的边上的相似点？如果是，请说明理由；如果不是，请找出一个不存在边上相似点的三角形；

    特例分析

    ③已知P为△ABC的边AB上的相似点，连接PC，若△ACP∽△ABC，则△ABC的形状是   ；

    ④如图③，在△ABC中，AB＝AC，∠A＝36°，P是边AB上的相似点，求的值．

    （2）在矩形ABCD中，AB＝a，BC＝b（a≥b）．P是AB上的点（P不与点A、点B重合），作PQ⊥CD，垂足为Q．如果矩形ADQP∽矩形ABCD，那么就称PQ为矩形ABCD的边AB、CD上的相似线．

    ①类比（1）中的“画法初探”，可以提出问题：对于如图④的矩形ABCD，在不限制画图工具的前提下，如何画出它的边AB、CD上的相似线PQ呢？

    你的解答是：   （只需描述PQ的画法，不需在图上画出PQ）．

    ②请继续类比（1）中的“辩证思考”、“特例分析”两个栏目对矩形的相似线进行研究，要求每个栏目提出一个问题并解决．

     

    查看答案和解析>>

    同步练习册答案