����⣺��1����y=0ʱ��
x
2-
x-4=0�����x
1=-2��x
2=8��
�ߵ�B�ڵ�A���Ҳ࣬
���A��������-2��0������B��������8��0����
��x=0ʱ��y=-4��
���C��������0��-4����
��2�������εĶԳ��Կ�֪����D������Ϊ��0��4����
��ֱ��BD�Ľ���ʽΪy=kx+b����
��
���k=-
��b=4��
��ֱ��BD�Ľ���ʽΪy=-
x+4��
��l��x�ᣬ
���M��������m��-
m+4������Q��������m��
m
2-
m-4����
��ͼ����MQ=DCʱ���ı���CQMD��ƽ���ı��Σ�
�ࣨ-
m+4��-��
m
2-
m-4��=4-��-4����
����ã�m
2-4m=0��
���m
1=0������������ȥ����m
2=4��
�൱m=4ʱ���ı���CQMD��ƽ���ı��Σ�
��ʱ���ı���CQBM��ƽ���ı��Σ�
�ⷨһ����m=4��
���P��OB���е㣮
��l��x�ᣬ
��l��y�ᣬ
���BPM�ס�BOD��
��
=
=
��
��BM=DM��
���ı���CQMD��ƽ���ı��Σ�
��DM
CQ��
��BM
CQ��
���ı���CQBM��ƽ���ı��Σ�
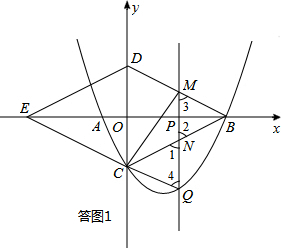
�ⷨ������ֱ��BC�Ľ���ʽΪy=k
1x+b
1����
��
���k
1=
��b
1=-4��
��ֱ��BC�Ľ���ʽΪy=
x-4��
�֡�l��x�ύBC�ڵ�N��
��x=4ʱ��y=-2��
���N��������4��-2����
�������֪����M������Ϊ��4��2������Q������Ϊ��4��-6����
��MN=2-��-2��=4��NQ=-2-��-6��=4��
��MN=QN��
�֡��ı���CQMD��ƽ���ı��Σ�
��DB��CQ��
���3=��4��
���ڡ�BMN���CQN�У�
��
���BMN�ա�CQN��ASA��
��BN=CN��
���ı���CQBM��ƽ���ı��Σ�
��3���������ϴ������������ĵ�Q���ֱ���Q
1��-2��0����Q
2��6��-4����
����BDQΪֱ�������Σ��������������Σ����ͼ2��ʾ��

���Ե�QΪֱ�Ƕ��㣮
��ʱ��BDΪֱ����Բ��Բ�������ߵĽ��㣬��Ϊ����֮Q�㣮
��P���߶�EB���˶�����-8��x
Q��8������ͼ�οɼ����ڴ˷�Χ�ڣ�Բ�������߲����㣬
�ʴ������β����ڣ�
���Ե�DΪֱ�Ƕ��㣮
����AD����OA=2��OD=4��OB=8��AB=10��
�ɹ��ɶ����ã�AD=
2��BD=
4��
��AD
2+BD
2=AB
2�����ABDΪֱ�������Σ�����AΪ����ĵ�Q��
��Q
1��-2��0����
���Ե�BΪֱ�Ƕ��㣮
��ͼ����Q
2��������x��y��������Q
2��Q
2K��x���ڵ�K����Q
2K=-y��OK=x��BK=8-x��
��֤��QKB�ס�BOD��
��
=����
=�������ã�y=2x-16��
�ߵ�Q���������ϣ���y=
x
2-
x-4��
��
x
2-
x-4=2x-16�����x=6��x=8��
��x=8ʱ����Q
2���B�غϣ�����ȥ��
��x=6ʱ��y=-4��
��Q
2��6��-4����

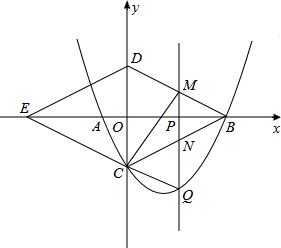 ��2013•̫ԭ���ۺ���̽����
��2013•̫ԭ���ۺ���̽����




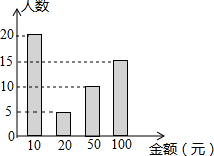 ��2013•̫ԭ���Ĵ��Ű����������ijУ�ţ�1����ѧ����չ�װ��Ļ����������������ͼ�Ǹð�ͬѧ��������ͳ��ͼ��д��һ�����ͼ������õ���Ϣ��
��2013•̫ԭ���Ĵ��Ű����������ijУ�ţ�1����ѧ����չ�װ��Ļ����������������ͼ�Ǹð�ͬѧ��������ͳ��ͼ��д��һ�����ͼ������õ���Ϣ�� ��2013•̫ԭ����ͼ����ʡij��һ���������ι��ţ��Ź�����ֱƽ���ڣ���ˮƽ�����ཻ��A��B���㣬������ߵ�C��AB�ľ���Ϊ9m��AB=36m��D��EΪ���ŵײ������㣬��DE��AB����E��ֱ��AB�ľ���Ϊ7m����DE�ij�Ϊ
��2013•̫ԭ����ͼ����ʡij��һ���������ι��ţ��Ź�����ֱƽ���ڣ���ˮƽ�����ཻ��A��B���㣬������ߵ�C��AB�ľ���Ϊ9m��AB=36m��D��EΪ���ŵײ������㣬��DE��AB����E��ֱ��AB�ľ���Ϊ7m����DE�ij�Ϊ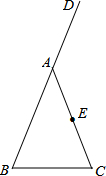 ��2013•̫ԭ����ͼ���ڡ�ABC�У�AB=AC��D��BA�ӳ����ϵ�һ�㣬��E��AC���е㣮
��2013•̫ԭ����ͼ���ڡ�ABC�У�AB=AC��D��BA�ӳ����ϵ�һ�㣬��E��AC���е㣮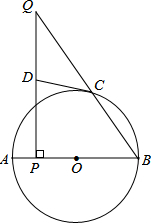 ��2013•̫ԭ����ͼ��ABΪ��O��ֱ������C�ڡ�O�ϣ���P��ֱ��AB�ϵ�һ�㣨����A�غϣ�������P��AB�Ĵ��߽�BC�ڵ�Q��
��2013•̫ԭ����ͼ��ABΪ��O��ֱ������C�ڡ�O�ϣ���P��ֱ��AB�ϵ�һ�㣨����A�غϣ�������P��AB�Ĵ��߽�BC�ڵ�Q��