
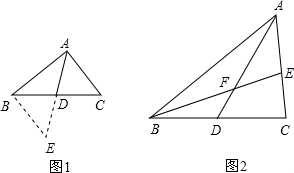
 某校数学课外兴趣小组活动时,老师提出如下问题:
某校数学课外兴趣小组活动时,老师提出如下问题:分析 (1)延长AD到点E,使DE=AD,根据SAS定理证明△ADC≌△EDB;
(2)根据全等三角形的性质得到BE=AC=6,根据三角形三边关系计算;
(3)延长AD到H,使DH=AD,根据全等三角形的性质得到BH=AC,∠BHD=∠CAD,根据等腰三角形的性质证明即可.
解答 (1)证明:∵延长AD到点E,使DE=AD,
在△ADC和△EDB中,
AD=ED,∠ADC=∠EDB(对顶角相等),CD=BD(中点定义),
∴△ADC≌△EDB(SAS),
故答案为:对顶角相等;SAS;
(2)解:∵△ADC≌△EDB,
∴BE=AC=6,
∴AB-BE<AE<AB+BE,即1<AD<7,
故答案为:1<AD<7;
(3)证明:延长AD到H,使DH=AD,
由(1)得,△ADC≌△HDB,
∴BH=AC,∠BHD=∠CAD,
∵AC=BF,
∴BH=BF,
∴∠BFD=∠BHD,
∴∠BFD=∠CAD.
点评 本题考查的是三角形的中线的概念和性质、全等三角形的判定和性质、三角形三边关系,掌握全等三角形的判定定理和性质定理是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\stackrel{→}{AB}$+$\stackrel{→}{CD}$=$\stackrel{→}{0}$ | B. | $\stackrel{→}{AB}$-$\stackrel{→}{AD}$=$\stackrel{→}{BD}$ | C. | $\stackrel{→}{AB}$+$\stackrel{→}{AD}$=$\stackrel{→}{BD}$ | D. | $\stackrel{→}{AB}$+$\stackrel{→}{BD}$=$\stackrel{→}{DA}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
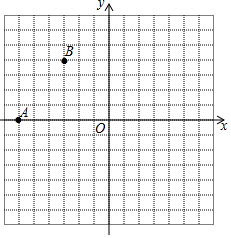 如图,在直角坐标平面内,已知点A的坐标(-6,0).
如图,在直角坐标平面内,已知点A的坐标(-6,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5×10-7m | B. | 5×10-8m | C. | 0.5×10-7m | D. | -5×108m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{{\begin{array}{l}{\frac{1-2x}{3}≤x+2}\\{2x+2>2({2x-1})}\end{array}}\right.$.把它的解集在数轴上表示出来,并写出这个不等式组的整数解.
解不等式组:$\left\{{\begin{array}{l}{\frac{1-2x}{3}≤x+2}\\{2x+2>2({2x-1})}\end{array}}\right.$.把它的解集在数轴上表示出来,并写出这个不等式组的整数解.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com