
 如图,正方形AOCB的边长为4,反比例函数y=$\frac{k}{x}$的图象过点E(3,4),与线段BC交于点D,直线y=-$\frac{1}{2}$x+b过点D,与线段AB相交于点F,连接OF,OE,请你探究∠AOF与∠EOC的数量关系,并证明.
如图,正方形AOCB的边长为4,反比例函数y=$\frac{k}{x}$的图象过点E(3,4),与线段BC交于点D,直线y=-$\frac{1}{2}$x+b过点D,与线段AB相交于点F,连接OF,OE,请你探究∠AOF与∠EOC的数量关系,并证明. 分析 根据反比例函数图象上点的坐标特征得k=12,则反比例函数的解析式y=$\frac{12}{x}$;再利用正方形的性质和反比例函数图象上点的坐标特征可确定D(4,3),根据函数图象上点的坐标特征可求出b=5,从而可确点F的坐标为(2,4),取BC的中点G,连结EG并延长交x轴于H,连结OG,如图,先证明△OAF≌△OCG得到∠AOF=∠2,接着证明△EGB≌△HGC得到EG=HG,EB=CH,然后证明OE=OH得到△OEH为等腰三角形,则根据等腰三角形的性质得OG平分∠EOG,即∠1=∠2,所以∠1=∠2=∠AOF,于是得到∠AOF=$\frac{1}{2}$∠EOC.
解答 解:∠AOF=$\frac{1}{2}$∠EOC.理由如下:
∵反比例函数的图象过点E(3,4),
∴k=3×4=12.
∴反比例函数的解析式y=$\frac{12}{x}$;
∵正方形AOCB的边长为4,
∴点D的横坐标为4,点F的纵坐标为4.
∵点D在反比例函数的图象上,
∴点D的纵坐标为3,即D(4,3),
∵点D在直线y=-$\frac{1}{2}$x+b上,
∴-$\frac{1}{2}$×4+b=3,解得b=5,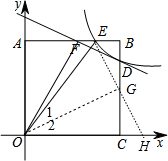
∴直线DF为y=-$\frac{1}{2}$x+5,
将y=4代入y=-$\frac{1}{2}$x+5,得4=-$\frac{1}{2}$x+5,解得x=2,
∴点F的坐标为(2,4),
取BC的中点G,连结EG并延长交x轴于H,连结OG,如图,
在△OAF和△OCG中,
$\left\{\begin{array}{l}{OA=OC}\\{∠OAF=∠OCG}\\{AF=CG}\end{array}\right.$,
∴△OAF≌△OCG(SAS),
∴∠AOF=∠2,
在△EGB和△HGC,
$\left\{\begin{array}{l}{∠B=∠GCH}\\{∠BGE=∠CGH}\\{BG=CG}\end{array}\right.$,
∴△EGB≌△HGC(ASA),
∴EG=HG,EB=CH,
∵E(3,4),B(4,4),
∴BE=1,
∴CH=1,
∴OH=5,
在Rt△AOE中,OE=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴OE=OH,
∴△OEH为等腰三角形,
而EG=HG,
∴OG平分∠EOG,即∠1=∠2,
∴∠1=∠2=∠AOF,
∴∠AOF=$\frac{1}{2}$∠EOC.
点评 本题考查了反比例函数综合题:熟练掌握反比例函数图象上点的坐标特征和正方形的性质;会用待定系数法求一次函数及反比例函数的解析式;灵活运用等腰三角形的性质.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
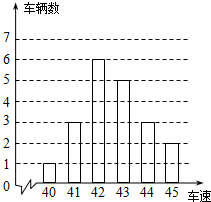 已知:如图,是交警在某个路口统计的某时段来往车辆的车速(单位:千米/时)情况.
已知:如图,是交警在某个路口统计的某时段来往车辆的车速(单位:千米/时)情况.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知正方形ABCD中,∠MAN=45°,且∠MAN的两边分别交BC、DC于点M、N.试猜想线段BM、DN和MN之间的数量关系,写出猜想,并加以证明.
已知正方形ABCD中,∠MAN=45°,且∠MAN的两边分别交BC、DC于点M、N.试猜想线段BM、DN和MN之间的数量关系,写出猜想,并加以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com