
【题目】一个菱形被一条直线分成面积为x,y的两部分,则y与x之间的函数图象只可能是( )
A.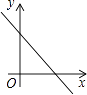
B.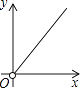
C.
D.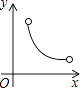
【答案】C
【解析】解:设菱形的面积为a(a是常数), 则根据题意得:x+y=a,
即y=﹣x+a,
当x=0时,y=a,当y=0时,x=a,
即连接点(a,0)和(0,a)即可得出函数的图象,
所以只有选项C符合,
故选C.
【考点精析】通过灵活运用函数的图象和菱形的性质,掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的有理数为﹣6,点B表示的有理数为6,点P从点A出发以每秒4个单位长度的速度在数轴上由A向B运动,当点P到达点B后立即返回,仍然以每秒4个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒).
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,请求出所有满足条件的t值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(0,3),点B的坐标为(4,0),C为第一象限内一点,AC⊥y轴,BC⊥x轴,D坐标为(m,0)(0<m<4).
(1)若D为OB的中点,求直线DC的解析式;
(2)若△ACD为等腰三角形,求m的值;
(3)E为四边形OACB的某一边上一点.
①若E在边BC上,满足△AOD≌△DBE,求m的值;
②若使△EOD为等腰三角形的点E有且只有4个,直接写出符合条件的m的值.
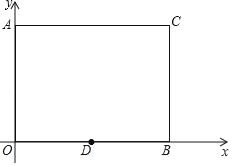
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
点A、B在数轴上分别表示两个数a、b,A、B两点间的距离记为|AB|,O表示原点.当A、B两点中有一点在原点时,不妨设点A为原点,如图1,则|AB|=|OB|=|b|=|a-b|;当A、B两点都不在原点时,

①如图2,若点A、B都在原点的右边时,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
②如图3,若点A、B都在原点的左边时,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
③如图4,若点A、B在原点的两边时,|AB|=|OB|+|OA|=|b|+|a|=-b+a=|a-b|.
回答下列问题:
(1)综上所述,数轴上A、B两点间的距离为|AB|=______.
(2)若数轴上的点A表示的数为3,点B表示的数为-4,则A、B两点间的距离为______;
(3)若数轴上的点A表示的数为x,点B表示的数为-2,则|AB|=______,若|AB|=3,则x的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
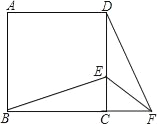
【题目】如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.
(1)求证:△BCE≌△DCF;
(2)若∠BEC=60°,求∠EFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.

(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题: 某校师生捐书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | 12 | 30% |
B.文学类 | n | 35% |
C.艺术类 | m | 20% |
D.其它类 | 6 | 15% |
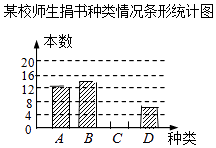
(1)统计表中的n= , 并补全条形统计图;
(2)本次活动师生共捐书2000本,请估计有多少本科普类图书?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com