
【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)如图1,若该抛物线经过原点O,且a=﹣ ![]() .
.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;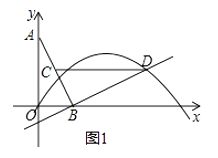
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是4个,请直接写出a的取值范围.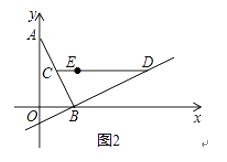
【答案】
(1)解:①过点D作DF⊥x轴于点F,如图1,
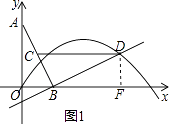
∵∠DBF+∠ABO=90°,∠BAO+∠ABO=90°,
∴∠DBF=∠BAO,
又∵∠AOB=∠BFD=90°,AB=BD,
在△AOB和△BFD中,
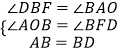 ,
,
∴△AOB≌△BFD(AAS)
∴DF=BO=1,BF=AO=2,
∴D的坐标是(3,1),
根据题意,得a=﹣ ![]() ,c=0,且a×32+b×3+c=1,
,c=0,且a×32+b×3+c=1,
∴b= ![]() ,
,
∴该抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x;
x;
②∵点A(0,2),B(1,0),点C为线段AB的中点,
∴C( ![]() ,1),
,1),
∵C、D两点的纵坐标都为1,
∴CD∥x轴,
∴∠BCD=∠ABO,
∴∠BAO与∠BCD互余,
要使得∠POB与∠BCD互余,则必须∠POB=∠BAO,
设P的坐标为(x,﹣ ![]() x2+
x2+ ![]() x),
x),
(Ⅰ)当P在x轴的上方时,过P作PG⊥x轴于点G,如图2,
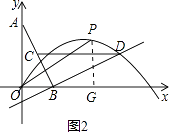
则tan∠POB=tan∠BAO,即 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,解得x1=0(舍去),x2=
,解得x1=0(舍去),x2= ![]() ,
,
∴﹣ ![]() x2+
x2+ ![]() x=
x= ![]() ,
,
∴P点的坐标为( ![]() ,
, ![]() );
);
(Ⅱ)当P在x轴的下方时,过P作PG⊥x轴于点G,如图3
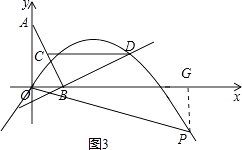
则tan∠POB=tan∠BAO,即 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,解得x1=0(舍去),x2=
,解得x1=0(舍去),x2= ![]() ,
,
∴﹣ ![]() x2+
x2+ ![]() x=﹣
x=﹣ ![]() ,
,
∴P点的坐标为( ![]() ,﹣
,﹣ ![]() );
);
综上,在抛物线上是否存在点P( ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() ),使得∠POB与∠BCD互余
),使得∠POB与∠BCD互余
(2)解:如图3,
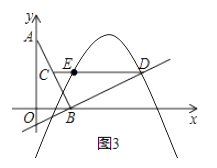
∵D(3,1),E(1,1),
抛物线y=ax2+bx+c过点E、D,代入可得 ![]() ,解得
,解得 ![]() ,所以y=ax2﹣4ax+3a+1.
,所以y=ax2﹣4ax+3a+1.
分两种情况:
①当抛物线y=ax2+bx+c开口向下时,若满足∠QOB与∠BCD互余且符合条件的Q点的个数是4个,则点Q在x轴的上、下方各有两个.
(i)当点Q在x轴的下方时,直线OQ与抛物线有两个交点,满足条件的Q有2个;
(ii)当点Q在x轴的上方时,要使直线OQ与抛物线y=ax2+bx+c有两个交点,抛物线y=ax2+bx+c与x轴的交点必须在x轴的正半轴上,与y轴的交点在y轴的负半轴,所以3a+1<0,解得a<﹣ ![]() ;
;
②当抛物线y=ax2+bx+c开口向上时,点Q在x轴的上、下方各有两个,
(i)当点Q在x轴的上方时,直线OQ与抛物线y=ax2+bx+c有两个交点,符合条件的点Q有两个;
(ii)当点Q在x轴的下方时,要使直线OQ与抛物线y=ax2+bx+c有两个交点,符合条件的点Q才两个.
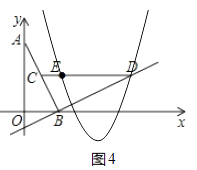
根据(2)可知,要使得∠QOB与∠BCD互余,则必须∠QOB=∠BAO,
∴tan∠QOB=tan∠BAO= ![]() =
= ![]() ,此时直线OQ的斜率为﹣
,此时直线OQ的斜率为﹣ ![]() ,则直线OQ的解析式为y=﹣
,则直线OQ的解析式为y=﹣ ![]() x,要使直线OQ与抛物线y=ax2+bx+c有两个交点,所以方程ax2﹣4ax+3a+1=﹣
x,要使直线OQ与抛物线y=ax2+bx+c有两个交点,所以方程ax2﹣4ax+3a+1=﹣ ![]() x有两个不相等的实数根,所以△=(﹣4a+
x有两个不相等的实数根,所以△=(﹣4a+ ![]() )2﹣4a(3a+1)>0,即4a2﹣8a+
)2﹣4a(3a+1)>0,即4a2﹣8a+ ![]() >0,解得a>
>0,解得a> ![]() (a<
(a< ![]() 舍去)
舍去)
综上所示,a的取值范围为a<﹣ ![]() 或a>
或a> ![]() .
.
【解析】(1)①过点D作DF⊥x轴于点F,先依据AAS证明△AOB≌△BFD,从而可得到D的坐标,然后将点D的坐标代入到抛物线的解析式求解即可;②先证得CD∥x轴,故此可得到∠POB=∠BAO,设P的坐标为(x,-![]() x2+
x2+![]() x),分为P在x轴的上方,P在x轴的下方两种情况画出图形,过P作PG⊥x轴于点G,然后依据锐角三角函数的定义列比例式求解即可;
x),分为P在x轴的上方,P在x轴的下方两种情况画出图形,过P作PG⊥x轴于点G,然后依据锐角三角函数的定义列比例式求解即可;
(2)如果使得符合条件的Q点的个数是4个,那么当a<0时,抛物线交于y轴的负半轴,当a>0时,最小值得<-1,接下来,解关于a的不等式即可.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,交AC于点E,连接CD,则CD=( )
A.3
B.4
C.4.8
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中,且A![]() 、B
、B![]() 、C
、C![]() .将其平移后得到
.将其平移后得到![]() ,若A,B的对应点是
,若A,B的对应点是![]() ,
,![]() ,C的对应点
,C的对应点![]() 的坐标是
的坐标是![]() .
.
(1)在平面直角坐标系中画出△ABC;
(2)写出点![]() 的坐标是_____________,
的坐标是_____________,![]() 坐标是___________;
坐标是___________;
(3)此次平移也可看作![]() 向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
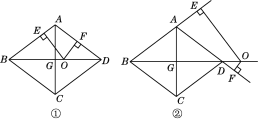
【题目】如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)求对角线AC的长及菱形ABCD的面积.
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度 y(cm)与所挂物体的质量 x(kg)之间有如下表关系:

下列说法不正确的是( )
A.y 随 x 的增大而增大B.所挂物体质量每增加 1kg弹簧长度增加 0.5cm
C.所挂物体为 7kg时,弹簧长度为 13.5cmD.不挂重物时弹簧的长度为 0cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,∠A=35°,∠C=40°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在射线DM上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低。马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元,A,B两种产品原来的运费和现在的运费(单位:元∕件)如下表所示:
品种 | A | B |
原来的运费 | 45 | 25 |
现在的运费 | 30 | 20 |
(1)求每次运输的农产品中A,B产品各有多少件?
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
2018年10月24日港珠澳大桥正式开通,它是中国建设史上里程最长、投资最多、施工难度最大的跨海桥梁项目,体现了我国逢山开路、遇水架桥的奋斗精神,体现了我国综合国力、自主创新能力,体现了我国勇创世界一流的民族志气. 港珠澳大桥全长55公里,跨越伶仃洋,东接香港特别行政区,西接广东省珠海市和澳门特别行政区,首次实现了珠海、澳门与香港的跨海陆路连接,极大地缩短了三地间的距离. 通车前,小亮妈妈驾车从香港到珠海的陆路车程大约220公里,如果行驶的平均速度不变,港珠澳大桥通车后,小亮妈妈驾车从香港到珠海所用的行驶时间比原来缩短了2小时15分钟,求小亮妈妈原来驾车从香港到珠海需要多长时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com