
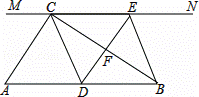
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.


(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即C E∥AD,
E∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
(3)当∠A=45°时,四边形B°ECD是正方形,理由是:
解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴四边形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.




 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
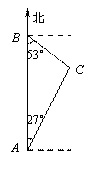
禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
 (参考数据:sin27°≈
(参考数据:sin27°≈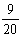 ,cos27°≈
,cos27°≈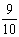 ,tan27°≈
,tan27°≈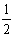 ,sin53°≈
,sin53°≈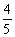 ,
, cos53°≈
cos53°≈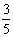 ,tan53°≈
,tan53°≈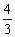 )
)


查看答案和解析>>
科目:初中数学 来源: 题型:
在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为 m.



查看答案和解析>>
科目:初中数学 来源: 题型:
现测得齐齐哈尔市扎龙自然保护区六月某5天的最高气温分别为27、30、27、32、34(单位:℃).这组数据的众数和中位数分别是 ( )
A. 34、27 B.27、30 C.27 、34 D.30、27
查看答案和解析>>
科目:初中数学 来源: 题型:
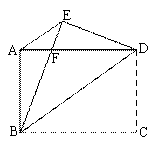
如图,四边形ABCD是矩形,AB=6cm,BC=8cm,把矩形沿直线BD折叠,点C落在点E处,BE与AD相交于点F,连接AE.下列结论:①△FBD是等腰三角形;②四边形ABDE是等腰梯形; ③图中有6对全等三角形;④四边形BCDF的周长为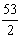 ;⑤AE的长为
;⑤AE的长为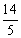 cm.其中结论正确的个数为 ( )
cm.其中结论正确的个数为 ( )
A.2个 B.3个 C.4个 D.5个
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产B产品不少于38件,问符合生产条件的生产方案由哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低?
(成本=材料费+加工费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com