【题目】如图，菱形ABOC的AB，AC分别与⊙O相切于点D、E，若点D是AB的中点，则∠DOE=__________.
【答案】60°
【解析】由AB，AC分别与⊙O相切于点D、E，可得∠BDO=∠ADO=∠AEO=90°，根据已知条件可得到BD=
OB，在Rt△OBD中，求得∠B=60°，继而可得∠A=120°，再利用四边形的内角和即可求得∠DOE的度数.
【详解 】∵AB，AC分别与⊙O相切于点D、E，
∴∠BDO=∠ADO=∠AEO=90°，
∵四边形ABOC是菱形，∴AB=BO，∠A+∠B=180°，
∵BD=AB，
∴BD=OB，
在Rt△OBD中，∠ODB=90°，BD=OB，∴cos∠B=
，∴∠B=60°，
∴∠A=120°，
∴∠DOE=360°-120°-90°-90°=60°，
故答案为：60°.
学业测评一课一测系列答案科目：初中数学 来源： 题型：
【题目】在一张长12cm、宽5cm的矩形纸片内，要折出一个菱形．小华同学按照取两组对边中点的方法折出菱形EFGH（见方案一），小丽同学沿矩形的对角线AC折出∠CAE=∠CAD，∠ACF=∠ACB的方法得到菱形AECF（见方案二）．
（1）你能说出小华、小丽所折出的菱形的理由吗？
（2）请你通过计算，比较小华和小丽同学的折法中，哪种菱形面积较大？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠ACB=90°，AD平分∠BAC，DE⊥AB于E．
（1）若∠BAC=50°，求∠EDA的度数；
（2）求证：直线AD是线段CE的垂直平分线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点，若点D为BC边的中点，点M为线段EF上一动点，则
周长的最小值为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）一般地，数轴上表示数m和数n的两点之间的距离等于
.如果表示数a和
的两点之间的距离是5，那么
__________；
（2）若数轴上表示数a的点位于与6之间，求
的值；
（3）当a取何值时，
的值最小，最小值是多少？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
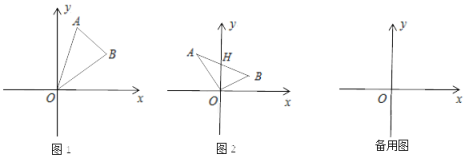
【题目】在平面直角坐标系中，O为坐标原点，A(m,n+1),B(m+2,n).
（1）当m=1,n=2时.如图1，连接AB、AO、BO.直接写出△ABO的面积为 .
（2）如图2，若点A在第二象限、点B在第一象限，连接AB、AO、BO,AB交y轴于H，△ABO的面积为2.求点H的坐标.
（3）若点A、B在第一象限，在y 轴正半轴上存在点C，使得∠CAB=900,且CA=AB,求m的值，及OC的长（用含n的式子表示）.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
