
【题目】如图,在平行四边形ABCD中,点P是对角线AC上的一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
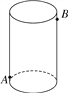
【题目】如图,圆柱形玻璃容器高19cm,底面周长为60cm,在外侧距下底1.5cm的点A处有一只蜘蛛,在蜘蛛正对面的圆柱形容器的外侧,距上底1.5cm处的点B处有一只苍蝇,蜘蛛急于捕捉苍蝇充饥,请你帮蜘蛛计算它沿容器侧面爬行的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.
(1) 用“列表法”或“树状图法”表示所有可能出现的结果;
(2) 小刚抽到物理实验B和化学实验F(记作事件P)的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设 ![]() =n.
=n.
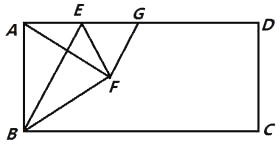
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
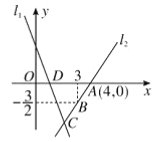
【题目】如图,直线![]() 的解析表达式为
的解析表达式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() ,直线
,直线![]() 交于点
交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的和最小,直接写出
的和最小,直接写出![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为 60°,然后在坡顶D测得树顶B的仰角为300,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是( ) m

A. ![]() B. 30 C.
B. 30 C. ![]() D. 40
D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF中,AB=DE,∠B=∠DEF.
(1)请你只添加一个条件(不再加辅助线),使△ABC≌△EFD,你添加的条件是 ;
(2)添加了条件后,证明△ABC≌△EFD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,则巡逻船从出发到成功拦截捕鱼船所用的时间是( )

A. 1小时 B. 2小时 C. 3小时 D. 4小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com