Ω‚¥£∫Ω‚£∫£®1£©°þA£®-1£¨
£©£¨
°ýOA=
=2£ª
°þOA»∆OÀ≥ ±’Ζ˝◊™120°„µ√OB£¨
°ýOB=OA=2£¨«“B‘⁄x÷·’˝∞Î÷·…œ£¨
°ýB£®2£¨0£©£Æ
£®2£©”…”⁄≈◊ŒÔœþπ˝‘≠µ„£¨ø……Ë∆‰Ω‚Œˆ ΩŒ™y=ax
2+bx£¨¥˙»ÎA£®-1£¨
£©°¢B£®2£¨0£©£¨µ√£∫
£¨Ω‚µ√
°ý≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=
x
2-
£Æ
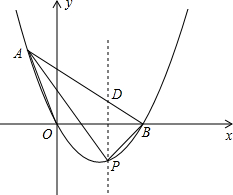
£®3£©…ËP£®x£¨
x
2-
£©£®0£ºx£º2£©£¨π˝P◊˜PD°Œy÷·Ωªœþ∂ŒAB”⁄D£ª
…Ë÷±œþAB£∫y=kx+b£®k°Ÿ0£©£¨Ω´A£®-1£¨
£©°¢B£®2£¨0£©¥˙»Î£¨µ√£∫
£¨Ω‚µ√
°ý÷±œþAB£∫y=-
x+
£¨‘Úµ„Dµƒ◊¯±Í£®x£¨-
x+
£©£ª
°ýPD=£®-
x+
£©-£®
x
2-
£©=-
x
2+
x+
£¨
°ýS
°˜APB=
°¡£®-
x
2+
x+
£©°¡3=-
x
2+
x+
£ª
S «πÿ”⁄xµƒ∂˛¥Œ∫Ø ˝£¨«“ø™ø⁄œÚœ¬£¨∂‘≥∆÷·x=
‘⁄0£ºx£º2µƒ∑∂Œßƒ⁄£¨“Ú¥Àµ±x=
±£¨°˜PABµƒ√ʪ˝◊Ó¥Û£¨«“◊Ó¥Û÷µŒ™
£ª
¥À ±Pµ„µƒ◊¯±Í£®
£¨-
£©£Æ
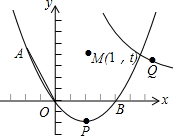
£®4£©µ„Q”Î≈◊ŒÔœþ…œµƒµ„A£®-1£¨
£©πÿ”⁄µ„M£®1£¨t£©≥…÷––ƒ∂‘≥∆£¨À˘“‘µ„Qµƒ∫·◊¯±Í±ÿŒ™3£ª
¢ŸBQŒ™Rt°˜QABµƒ÷±Ω«±þ ±£¨BQ°ÕAB£¨º¥£∫k
AB°¡k
BQ=-1£¨Ω‚µ√£∫k
BQ=
£ª
ø……Ë÷±œþBQ£∫y=
x+b£¨¥˙»ÎB£®2£¨0£©£¨µ√£∫b=-2
£¨
°ý÷±œþBQ£∫y=
x-2
£¨µ±x=3 ±£¨y=
£¨º¥ Q£®3£¨
£©£ª
Ω´µ„Qµƒ◊¯±Í¥˙»Î∑¥±»¿˝∫Ø ˝µƒΩ‚Œˆ Ω÷–£¨µ√£∫k
1=xy=3
£ª
¢⁄AQŒ™Rt°˜AOBµƒ÷±Ω«±þ ±£¨AQ°ÕAB£¨Õ¨¢Ÿø…«Ûµ√£∫k
2=15
£ª
◊€…œ£¨∑˚∫œÃıº˛µƒ∑¥±»¿˝∫Ø ˝Ω‚Œˆ ΩŒ™£∫y=
ªÚy=
£Æ

 »ÁÕº£¨‘⁄÷±Ω«◊¯±Íœµ÷–£¨µ„Aµƒ◊¯±ÍŒ™£®-1£¨
»ÁÕº£¨‘⁄÷±Ω«◊¯±Íœµ÷–£¨µ„Aµƒ◊¯±ÍŒ™£®-1£¨ £®3£©…ËP£®x£¨
£®3£©…ËP£®x£¨



 »ÁÕº£¨‘⁄÷±Ω«◊¯±Íœµ÷–£¨µ„Pµƒ◊¯±ÍŒ™£®3£¨4£©£¨Ω´OP»∆‘≠µ„OƒÊ ±’Ζ˝◊™90°„µ√µΩœþ∂ŒOP°‰£Æ
»ÁÕº£¨‘⁄÷±Ω«◊¯±Íœµ÷–£¨µ„Pµƒ◊¯±ÍŒ™£®3£¨4£©£¨Ω´OP»∆‘≠µ„OƒÊ ±’Ζ˝◊™90°„µ√µΩœþ∂ŒOP°‰£Æ

 £¨2£©£Æª≠≥ˆ°˜ABCµƒ¡Ω∏ˆŒªÀ∆Õº–Œ°˜A1B1C1£¨°˜A2B2C2£¨Õ¨ ±¬˙◊„œ¬¡–¡Ω∏ˆÃıº˛£∫
£¨2£©£Æª≠≥ˆ°˜ABCµƒ¡Ω∏ˆŒªÀ∆Õº–Œ°˜A1B1C1£¨°˜A2B2C2£¨Õ¨ ±¬˙◊„œ¬¡–¡Ω∏ˆÃıº˛£∫