
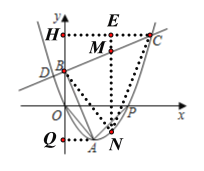
【题目】如图,△OAP是等腰直角三角形,∠OAP=90°,点A在第四象限,点P坐标为(8,0),抛物线y=ax2+bx+c经过原点O和A、P两点.

(1)求抛物线的函数关系式.
(2)点B是y轴正半轴上一点,连接AB,过点B作AB的垂线交抛物线于C、D两点,且BC=AB,求点B坐标;
(3)在(2)的条件下,点M是线段BC上一点,过点M作x轴的垂线交抛物线于点N,求△CBN面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先根据![]() 是等腰直角三角形,
是等腰直角三角形,![]() 和点P的坐标求出点A的坐标,再利用待定系数法即可求得;
和点P的坐标求出点A的坐标,再利用待定系数法即可求得;
(2)设点![]() ,如图(见解析),过点C作CH垂直y轴于点H,过点A作AQ垂直y轴于点Q,易证明
,如图(见解析),过点C作CH垂直y轴于点H,过点A作AQ垂直y轴于点Q,易证明![]() ,可得
,可得![]() ,则点C坐标为
,则点C坐标为![]() ,将其代入题(1)中的抛物线函数关系式即可得;
,将其代入题(1)中的抛物线函数关系式即可得;
(3)如图,延长NM交CH于点E,则![]() ,先通过点B、C求出直线BC的函数关系式,因点N在抛物线上,则设
,先通过点B、C求出直线BC的函数关系式,因点N在抛物线上,则设![]() ,则可得点M的坐标,再根据三角形的面积公式列出等式,利用二次函数的性质求最值即可.
,则可得点M的坐标,再根据三角形的面积公式列出等式,利用二次函数的性质求最值即可.
(1)![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点P坐标为
,点P坐标为![]()
则点A的坐标为![]()
将点O、A、B三点坐标代入抛物线的函数关系式得:
 ,解得:
,解得:
故抛物线的函数关系式为:![]() ;
;
(2)设点![]() ,过点C作CH垂直y轴于点H,过点A作AQ垂直y轴于点Q,
,过点C作CH垂直y轴于点H,过点A作AQ垂直y轴于点Q,
![]()
![]()
又![]()
![]()
![]()
故点C的坐标为![]()
将点C的坐标代入题(1)的抛物线函数关系式得:
![]() ,解得:
,解得:![]()
故点B的坐标为![]() ;
;

(3)如图,延长NM交CH于点E,则![]()
设直线BC的解析式为:![]() ,将点
,将点![]() ,点
,点![]() 代入得:
代入得:
![]() 解得:
解得:![]()
则直线BC的解析式为:![]()
因点N在抛物线上,设![]() ,则点M的坐标为
,则点M的坐标为![]()
![]() 的面积
的面积![]()
即![]()
整理得:![]()
又因点M是线段BC上一点,则![]()
由二次函数的性质得:当![]() 时,y随x的增大而增大;当
时,y随x的增大而增大;当![]() 时,y随x的增大而减小
时,y随x的增大而减小
故当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.


科目:初中数学 来源: 题型:
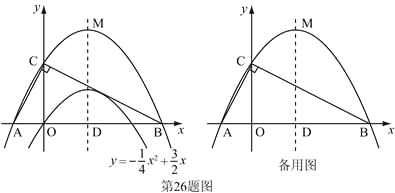
【题目】(本题满分12分)已知二次函数![]() 的图象如图.
的图象如图.
(1)求它的对称轴与![]() 轴交点D的坐标;
轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与![]() 轴,
轴,![]() 轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
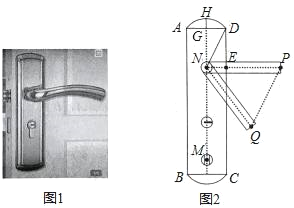
【题目】小明家的门框上装有一把防盗门锁(如图1).其平面结构图如图2所示,锁身可以看成由两条等弧AD,弧BC和矩形ABCD组成,弧BC的圆心是倒锁按钮点M.已知弧AD的弓形高GH=2cm,AD=8cm,EP=11cm.当锁柄PN绕着点N旋转至NQ位置时,门锁打开,此时直线PQ与弧BC所在的圆相切,且PQ∥DN,tan∠NQP=2.
(1)弧BC所在圆的半径为_____cm.
(2)线段AB的长度约为_____cm.(![]() ≈2.236,结果精确到0.1cm)
≈2.236,结果精确到0.1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图.请你根据统计图回答下列问题:
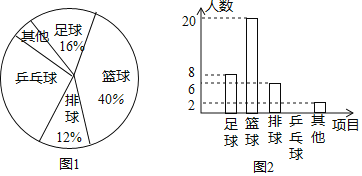
(1)请补全条形统计图(图2);
(2)在扇形统计图中,“篮球”部分所对应的圆心角是____________度?
(3)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
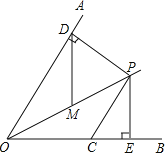
【题目】如图,已知OP平分∠AOB,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.CP=![]() ,PD=6.如果点M是OP的中点,则DM的长是_____.
,PD=6.如果点M是OP的中点,则DM的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中,装有2个白球,1个红球,1个黄球,这些球除颜色外都相同.请用列表法或画树形图法求下列事件的概率:
(1)搅匀后从中任意摸出1个球,恰好是白球.
(2)搅匀后从中任意摸出2个球,2个都是白球.
(3)再放入几个除颜色外都相同的黑球,搅匀后从中任意摸出1个球,恰好是黑球的概率为![]() ,求放入了几个黑球?
,求放入了几个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的一种商品其售价是成本的1.5倍,当售价降低5元时商品的利润率为25%.若不进行任何推广年销售量为1万件.为了获得更好的利益,公司准备拿出一定的资金做推广,根据经验,每年投入的推广费x万元时销售量y(万件)是x的二次函数:当x为1万元时,y是1.5(万件).当x为2万元时,y是1.8(万件).
(1)求该商品每件的的成本与售价分别是多少元?
(2)求出年利润与年推广费x的函数关系式;
(3)如果投入的年推广告费为1万到3万元(包括1万和3万元),问推广费在什么范同内,公司获得的年利润随推广费的增大而增大?
查看答案和解析>>
科目:初中数学 来源: 题型:
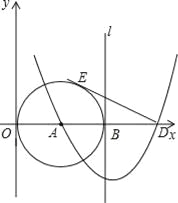
【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求此切线长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com