
某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元.设第二个月单价降低x元.
(1)填表(用含x的代数式表示)
(2)如果批发商希望通过销售这批T恤获利8750元,那么第二个月的单价应是多少元?
(3)要使批发商获利最多,那么第二个月的单价应是多少元,此时获得的最大利润是多少元?请说明理由,并写出必要的过程.
(1)由题意得
(2)75元或65元;(3)当第二个月的单价是70元时,获得的最大利润是9000元.
解析试题分析:(1)根据“单价每降低1元,可多售出10件”即可得到结果;
(2)根据(1)中表格中的代数式及销售这批T恤获利8750元即可列方程求解;
(3)先表示出第二个月的获得的利润的函数关系式,再根据二次函数的性质求解即可.
(1)由题意得
(2)由题意得(80-50)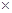 200+(80-50-x)(200+10x)–(50-40)(800-200-200-10x)="8750"
200+(80-50-x)(200+10x)–(50-40)(800-200-200-10x)="8750"
整理,得x2-20x+75=0,解这个方程得x1=5,x2=15.
答:第二个月的单价应是75元或65元;
(3)第二个月的获得的利润=(80-50)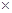 200+(80-50-x)(200+10x)–(50-40)(800-200-200-10x)
200+(80-50-x)(200+10x)–(50-40)(800-200-200-10x)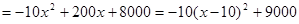
当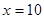 ,即第二个月的单价是60+10=70元时,获得的最大利润是9000元.
,即第二个月的单价是60+10=70元时,获得的最大利润是9000元.
考点:二次函数的应用
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 每件T恤的利润(元) | 销售量(件) | |
| 第一个月 | 20-x 20-x |
200+10x 200+10x |
| 清仓时 | -10 -10 |
200-10x 200-10x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | ▲ | 40 |
| 销售量(件) | 200 | ▲ | ▲ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com