
如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.
(1)若四边形ABCD是菱形,则它的中点四边形EFGH一定是 ;
A.菱形 B.矩形 C.正方形 D.梯形
(2)若四边形ABCD的面积为S1,中点四边形EFGH的面积记为S2,则S1与S2的数量关系是S1= S2
(3)在四边形ABCD中,沿中点四边形EFGH的其中三边剪开,可得三个小三角形,将这三个小三角形与原图中未剪开的小三角形拼接成一个平行四边形,请在答题卡的图形上画出一种拼接示意图,并写出对应全等的三角形.

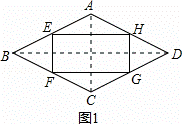
解:(1)如图1,连接AC、BD.
∵E、F、G、H分别是菱形ABCD各边的中点,
∴EH∥BD∥FG,EF∥AC∥HG,EH=FG=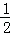 BD,EF=HG=
BD,EF=HG=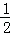 AC,
AC,
∴四边形EFGH为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴EF⊥FG,
∴▱EFGH是矩形;
故选:B.
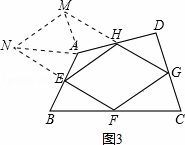
(2)如图2,设AC与EH、FG分别交于点N、P,BD与EF、HG分别交于点K、Q,
∵E是AB的中点,EF∥AC,EH∥BD,
∴△EBK∽△ABM,△AEN∽△EBK,
∴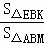 =
=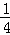 ,S△AEN=S△EBK,
,S△AEN=S△EBK,
∴ =
=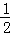 ,同理可得
,同理可得 =
=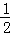 ,
, =
=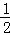 ,
, =
=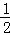 ,
,
∴ =
=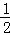 ,
,
∴四边形ABCD的面积为S1,中点四边形EFGH的面积记为S2,则S1与S2的数量关系是S1=2S2;
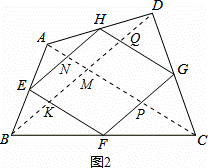
(3)如图3,四边形NEHM是平行四边形;
△MAH≌△GDH,△NAE≌△FBE,△CFG≌△ANM.


科目:初中数学 来源: 题型:
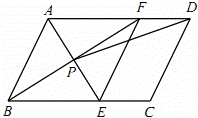
如图,在▱ABCD中,AE平分∠BAD,交BC于点E,BF平分ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
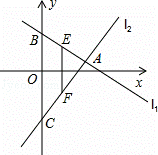
如图,已知直线l1:y=k1x+4与直线l2:y=k2x﹣5交于点A,它们与y轴的交点分别为点B,C,点E,F分别为线段AB、AC的中点,则线段EF的长度为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com