
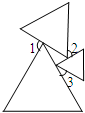
 三个等边三角形的位置如图所示,若∠1+∠3=122°,则∠2=
三个等边三角形的位置如图所示,若∠1+∠3=122°,则∠2= 解:∵图中是三个等边三角形,
解:∵图中是三个等边三角形,

科目:初中数学 来源: 题型:
 如图,正三角形ABC的边长为2,点A,B在半径为
如图,正三角形ABC的边长为2,点A,B在半径为| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,某工厂A前面有一条笔直的公路,原来有两条路AB,CD可以从工厂A到达公路,经测量AB=6千米,AC=8千米,BC=10千米,现需要修建一条公路,使工厂A到公路的距离最短.请你帮工厂A设计一种方案,并求出最短距离.
如图所示,某工厂A前面有一条笔直的公路,原来有两条路AB,CD可以从工厂A到达公路,经测量AB=6千米,AC=8千米,BC=10千米,现需要修建一条公路,使工厂A到公路的距离最短.请你帮工厂A设计一种方案,并求出最短距离.查看答案和解析>>
科目:初中数学 来源: 题型:
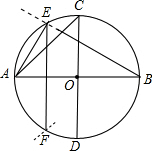 如图,在⊙O中,如果作两条互相垂直的直径AB、CD,那么弦AC是⊙O的内接正方形的一边;如果以点A为圆心,以OA为半径画弧,与⊙O相交于点E,F,那么弦AE、CE、EF分别是⊙O的内接正六边形、正十二边形、正三角形的一边,为什么?
如图,在⊙O中,如果作两条互相垂直的直径AB、CD,那么弦AC是⊙O的内接正方形的一边;如果以点A为圆心,以OA为半径画弧,与⊙O相交于点E,F,那么弦AE、CE、EF分别是⊙O的内接正六边形、正十二边形、正三角形的一边,为什么?查看答案和解析>>
科目:初中数学 来源: 题型:
| A、2个 | B、4个 | C、6个 | D、8个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com