
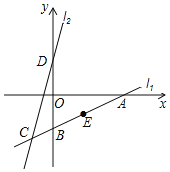
【题目】如图,直线l1:y=![]() x-4分别与x轴,y轴交于A,B两点,与直线l2交于点C(-2,m).点D是直线l2与y轴的交点,将点A向上平移3个单位,再向左平移8个单位恰好能与点D重合.
x-4分别与x轴,y轴交于A,B两点,与直线l2交于点C(-2,m).点D是直线l2与y轴的交点,将点A向上平移3个单位,再向左平移8个单位恰好能与点D重合.
(1)求直线l2的解析式;
(2)已知点E(n,-2)是直线l1上一点,将直线l2沿x轴向右平移.在平移过程中,当直线l2与线段BE有交点时,求平移距离d的取值范围.
【答案】(1)直线l2的解析式为y=4x+3;(2)![]() ≤d≤
≤d≤![]() .
.
【解析】
(1)根据平移的方向和距离即可得到A(8,0),D(0,3),再根据待定系数法即可得到直线l2的解析式;
(2)根据一次函数图象上点的坐标特征,即可得到E(4,-2),再根据y=![]() x-4中,令x=0,则y=-4,可得B(0,-4),依据直线l2与线段BE有交点,即可得到平移距离d的取值范围.
x-4中,令x=0,则y=-4,可得B(0,-4),依据直线l2与线段BE有交点,即可得到平移距离d的取值范围.
(1)∵将点A向上平移3个单位,再向左平移8个单位恰好能与点D重合,
∴点A离y轴8个单位,点D离x轴3个单位,
∴A(8,0),D(0,3),
把点C(-2,m)代入l1:y=![]() x-4,可得
x-4,可得
m=-1-4=-5,
∴C(-2,-5),
设直线l2的解析式为y=kx+b,
把D(0,3),C(-2,-5),代入可得
![]() ,解得
,解得![]() ,
,
∴直线l2的解析式为y=4x+3;
(2)把E(n,-2)代入直线l1:y=![]() x-4,可得
x-4,可得
-2=![]() n-4,
n-4,
解得n=4,
∴E(4,-2),
在y=![]() x-4中,令x=0,则y=-4,
x-4中,令x=0,则y=-4,
∴B(0,-4),
设直线l2沿x轴向右平移后的解析式为y=4(x-n)+3,
当平移后的直线经过点B(0,-4)时,-4=4(0-n)+3,
解得n=![]() ;
;
当平移后的直线经过点E(4,-2)时,-2=4(4-n)+3,
解得n=![]() .
.
∵直线l2与线段BE有交点,
∴平移距离d的取值范围为:![]() ≤d≤
≤d≤![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
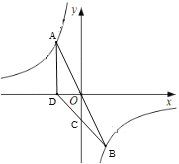
【题目】如图,直线y=mx与双曲线y=![]() 交于A、B两点,D为x轴上一点,连接BD交y轴与点C,若C(0,-2)恰好为BD中点,且△ABD的面积为6,则B点坐标为__________.
交于A、B两点,D为x轴上一点,连接BD交y轴与点C,若C(0,-2)恰好为BD中点,且△ABD的面积为6,则B点坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店用1050元购进第一批某种钢笔,很快卖完,又用1440元购进第二批该种钢笔,但第二批每支钢笔的进价是第一批进价的1.2倍,数量比第一批多了10支。
(1)求第一批每支钢笔的进价是多少元?
(2)第二批钢笔按24元/支的价格销售,销售一定数量后,根据市场情况,商店决定对剩余的钢笔全按8折一次性打折销售,但要求第二批钢笔的利润率不低于20%,问至少销售多少支后开始打折?
查看答案和解析>>
科目:初中数学 来源: 题型:
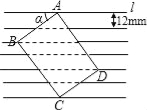
【题目】如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小丽一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.现有甲、乙两家租车公司,租车费用如下:甲公司按日收取固定租金80元,另外再按租车时间计费;乙公司无固定租金,直接按租车时间计费,每小时租费是30元.

(1)设租用时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,其图象如图所示,分别求出y1, y2关于x的函数解析式;
(2)请你帮助小丽计算,租用哪家新能源汽车自驾出游更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
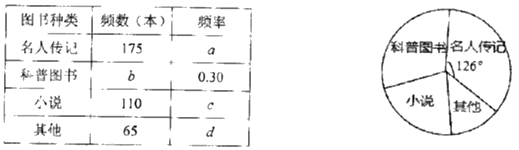
【题目】2019年5月区教育局在全区中小学开展了“情系新疆书香援疆”捐书活动.某学校学生社团对部分学生所捐图书进行统计,根据收集的数据绘制了下面不完整的统计图表.请你根据统计图表中所提供的信息解答下列问题:
(1)统计表中的![]() _____________,
_____________,![]() _____________,
_____________,![]() _____________,
_____________,![]() _____________;
_____________;
(2)科普图书在扇形统计图中的圆心角是_____________°;
(3)若该校共捐书1500本,请估算“科普图书”和“小说”一共多少本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(材料阅读)数轴是数学学习的一个很重要的工具,利用数轴可以将数与形完美结合.通过数轴我们可发现许多重要的规律:
①对值的几何意义:一般地,若点![]() 、点
、点![]() 在数轴上表示的有理数分别为
在数轴上表示的有理数分别为![]() ,
,![]() ,那么
,那么![]() 、
、![]() 两点之间的距离表示为
两点之间的距离表示为![]() ,记作
,记作![]() ,
,![]() 则表示数
则表示数![]() 和1在数轴上对应的两点之间的距离;又如
和1在数轴上对应的两点之间的距离;又如![]() ,所以
,所以![]() 表示数
表示数![]() 和
和![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;
②若数轴上点![]() 、点
、点![]() 表示的数分别为
表示的数分别为![]() 、
、![]() ,那么线段
,那么线段![]() 的中点
的中点![]() 表示的数为
表示的数为![]() .
.
(问题情境)如图,在数轴上,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 在原点右侧,表示的数为
在原点右侧,表示的数为![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度沿数轴正方向运动,同时,动点
个单位长度的速度沿数轴正方向运动,同时,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度沿数轴负方向运动,其中线段
个单位长度的速度沿数轴负方向运动,其中线段![]() 的中点记作点
的中点记作点![]() .
.
![]()
(综合运用)
(1)出发![]() 秒后,点
秒后,点![]() 和点
和点![]() 相遇,则
相遇,则![]() 表示的数
表示的数![]() ___________;
___________;
(2)在第(1)问的基础上,当![]() 时,求运动时间;
时,求运动时间;
(3)在第(1)问的基础上,点![]() 、
、![]() 在相遇后继续以原来的速度在这条数轴上运动,但
在相遇后继续以原来的速度在这条数轴上运动,但![]() 、
、![]() 两点运动的方向相同.随着点
两点运动的方向相同.随着点![]() 、
、![]() 的运动,线段
的运动,线段![]() 的中点
的中点![]() 也相应移动,问线段
也相应移动,问线段![]() 的中点
的中点![]() 能否与表示
能否与表示![]() 的点重合?若能,求出从
的点重合?若能,求出从![]() 、
、![]() 相遇起经过的运动时间;若不能,请说明理由.
相遇起经过的运动时间;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
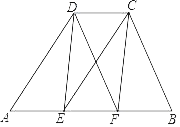
【题目】已知:如图,在四边形ABCD中,AB=3CD,AB∥CD,CE∥DA,DF∥CB.
(1)求证:四边形CDEF是平行四边形;
(2)填空:
①当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是矩形;
②当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx﹣k的图象的交点坐标为A(m,2).
(1)求m的值和一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,求△AOB的面积;
(3)直接写出使函数y=kx﹣k的值大于函数y=x的值的自变量x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com