设x1,x2,…,x2008是整数,且满足下列条件:
(1)-1≤xn≤2(n=1,2,…,2 008);
(2)x1+x2+…+x2008=200;
(3)x12+x22+…+x20082=2 008.
求x13+x23+…+x20083的最小值和最大值.
【答案】
分析:根据设x
1,x
2,…,x
2008中有q个0,r个-1,s个1,t个2,可得出等式即可求出x
13+x
23+…+x
20083取最大值2408.
解答:解:设x
1,x
2,…,x
2008中有q个0,r个-1,s个1,t个2.(2分)
则
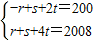
①(5分)
两式相加得s+3t=1104.故0≤t≤368.(10分)
由x
13+x
23+…+x
20083=-r+s+8t=6t+200,(12分)
得200≤x
13+x
23+…+x
20083≤6×368+200=2408.(15分)
由方程组①知:当t=0,s=1104,r=904时,
x
13+x
23+…+x
20083取最小值200; (17分)
当t=368,s=0,r=536时,
x
13+x
23+…+x
20083取最大值2408.(20分)
点评:此题主要考查了函数最值问题,根据已知求出200≤x
13+x
23+…+x
20083≤6×368+200=2408,即得出当t=368,s=0,r=536时最小值是解题关键.

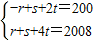 ①(5分)
①(5分)

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案