
分析 (1)根据a的值与零的大小关系,可判断开口方向,根据顶点坐标公式,可得对称轴、顶点坐标;
(2)根据a的值与零的大小关系,可判断开口方向,根据顶点坐标公式,可得对称轴、顶点坐标;
(3)根据a的值与零的大小关系,可判断开口方向,根据顶点坐标公式,可得对称轴、顶点坐标;
(4)根据a的值与零的大小关系,可判断开口方向,根据顶点坐标公式,可得对称轴、顶点坐标.
解答 解:(1)y=3x2+2x,a=3>0,抛物线开口向上,对称轴是x=-$\frac{b}{2a}$=-$\frac{1}{3}$,顶点横坐标是=-$\frac{b}{2a}$=-$\frac{1}{3}$,顶点的纵坐标是$\frac{4ac-{b}^{2}}{4a}$=$\frac{-{2}^{2}}{4×3}$=-$\frac{1}{3}$,顶点坐标是(-$\frac{1}{3}$,-$\frac{1}{3}$);
(2)y=-x2-2x,a=-1<0,抛物线开口向下,对称轴是x=-$\frac{b}{2a}$=-1,顶点横坐标是=-$\frac{b}{2a}$=-1,顶点的纵坐标是$\frac{4ac-{b}^{2}}{4a}$=$\frac{-(-2)^{2}}{-4}$=1,顶点坐标是(-1,1);
(3)y=-2x2+8x-8,a=-2<0,抛物线开口向下,对称轴是x=-$\frac{b}{2a}$=2,顶点横坐标是=-$\frac{b}{2a}$=4,顶点的纵坐标是$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×(-2)×(-8)-{8}^{2}}{4×(-2)}$=0,顶点坐标是(4,0);
(4)y=$\frac{1}{2}$x2-4x+3,a=$\frac{1}{2}$>0,抛物线开口向上,对称轴是x=-$\frac{b}{2a}$=4,顶点横坐标是=-$\frac{b}{2a}$=4,顶点的纵坐标是$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×\frac{1}{2}×3-(-4)^{2}}{4×\frac{1}{2}}$=-5,顶点坐标是(4,-5).
点评 本题考查了二次函数的性质,a>0,抛物线开口向上,对称轴是x=-$\frac{b}{2a}$,顶点横坐标是=-$\frac{b}{2a}$,顶点的纵坐标是$\frac{4ac-{b}^{2}}{4a}$,顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 若|a-b|=0,则a=b | |
| B. | 等式||m|+1|=|m|+1 | |
| C. | 若|-x|=|-7|,则x=±7 | |
| D. | 对一切有理数p,都一定有等式|-p|=p成立 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-{a^2}÷a•\frac{1}{a}=-{a^2}$ | B. | (a+2)2=a2+4 | C. | -(-a3)2=a6 | D. | (-a3b)2=a6b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
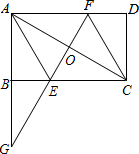 如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB至G,使BG=AB,连接GO交BC于点E,延长GO交AD于点F,判断四边形AECF的形状,并证明你的结论.
如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB至G,使BG=AB,连接GO交BC于点E,延长GO交AD于点F,判断四边形AECF的形状,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
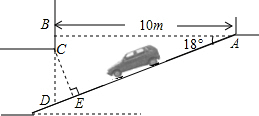 某商场为缓解我市“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说的对?请你判断并计算出正确的结果.(结果精确到0.1m)
某商场为缓解我市“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说的对?请你判断并计算出正确的结果.(结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com