
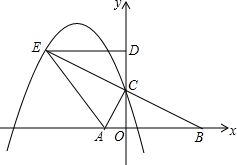
 如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.
如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.分析 (1)由题意得:BC=EC,∠ABC=∠DEC,又由AC⊥BE,根据线段垂直平分线的性质,可证得AB=AE,继而证得:CE平分∠AED;
(2)由∠ACB=90°,CO⊥AB,易证得:△AOC∽△COB,然后利用相似三角形的对应边成比例,求得OC的长,即可求得点C的坐标,再利用待定系数法求得函数的解析式;
(3)若以AC、CE为邻边,则点E可以看成点C向左平移4个单位,再向上平移2个单位,将点A向左平移4个单位,再向上平移2个单位得点P(-5,2),又可得点P在抛物线上;同理可得若以EC、EA为邻边,同理可得点P(3,-2),经验证此点不在抛物线上,故舍去;若以AC、AE为邻边,同理可得点P(-3,6),经验证此点不在抛物线上,故舍去.
解答 解:(1)由题意得:BC=EC,∠ABC=∠DEC.
∵AC⊥BE,
∴AB=AE,
∴∠AEB=∠ABC,
∴∠AEB=∠DEC,
即CE平分∠AED;
(2)∵∠ACB=90°,CO⊥AB,
∴∠AOC=∠COB=90°,∠ACO+∠BCO=90°,∠ACO+∠CAO=90°,
∴∠CAO=∠BCO,
∴△AOC∽△COB,
∴$\frac{OA}{OC}=\frac{OC}{OB}$,
∴OC2=OA•OB=4,
∴OC=2.
∴点C坐标为(0,2),点E坐标为(-4,4).
由$\left\{\begin{array}{l}{c=2}\\{-\frac{1}{2}×16-4b+c=4}\end{array}\right.$,
得$b=-\frac{5}{2}$,c=2,
∴所求抛物线解析式为$y=-\frac{1}{2}{x^2}-\frac{5}{2}x+2$.
(3)若以AC、CE为邻边,则点E可以看成点C向左平移4个单位,再向上平移2个单位,将点A向左平移4个单位,再向上平移2个单位得点P(-5,2).
当x=-5时,$y=-\frac{1}{2}×25-\frac{5}{2}×({-5})+2=2$,
∴点P在抛物线上.
∴点P(-5,2)即为所求;
若以EC、EA为邻边,同理可得点P(3,-2),经验证此点不在抛物线上,故舍去;
若以AC、AE为邻边,同理可得点P(-3,6),经验证此点不在抛物线上,故舍去;
∴点P的坐标为(-5,2).
点评 此题属于二次函数综合题,此题考查了待定系数法求函数的解析式、旋转的性质、相似三角形的判定与性质以及平行四边形的性质.注意旋转中的对应关系以及平行四边形中的平移性质.


科目:初中数学 来源: 题型:解答题
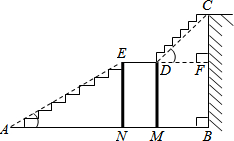 如图是某宾馆大厅到二楼的楼梯设计图,已知BC=5米,AB=8米,DM、EN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°.
如图是某宾馆大厅到二楼的楼梯设计图,已知BC=5米,AB=8米,DM、EN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com