
解:过点A作直线MN,使MN∥BC
∵MN∥BC
∴∠B=∠MAB,∠C=∠NBC(两直线平行,内错角相等)
∵∠MAB+∠NBC+∠BAC=180°(平角定义)
∴∠B+∠C+∠BAC=180°(等量代换)
即∠A+∠B+∠C=180°.
评价:两位同学都巧妙地通过作辅助线,第一位同学利用平角的定义,第二位同学利用角的和,方法简单,条理清晰.
分析:两名同学的证法都不对.因为“三角形一个外角等于和它不相邻的两个内角和”与“直角三角形两锐角互余”都是由三角形内角和定理推导的.
点评:要证明三角形的内角和等于180°即三角形三个内角的和是平角,就要作辅助线,使得三角形的三个内角的和转化成组成平角的三个角之和.

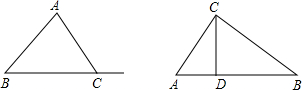
 解:过点A作直线MN,使MN∥BC
解:过点A作直线MN,使MN∥BC

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案