
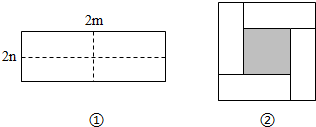
���� ƽ���ֳɺ�ÿ��С�����εij�Ϊm����Ϊn��
��1�������εı߳�=С�����εij�-����
��2����һ�ַ���Ϊ�������������-4��С������������ڶ��ֱ�ʾ����Ϊ����Ӱ����ΪС�����ε������
��3�����ã�m+n��2-4mn=��m-n��2����⣻
��4�����ã�a-b��2=��a+b��2-4ab����⣮
��� �⣺��1��ͼ���е���Ӱ���ֵ�С�����εı߳�=m-n��
��2�������٣�m+n��2-4mn��
�����ڣ�m-n��2��
��3������������ʽ֮��ĵ�����ϵ�ǣ�
��m-n��2=��m+n��2-4mn��
��4����a-b��2=��a+b��2-4ab��
��a+b=6��ab=5��
�ࣨa-b��2=36-20=16��
��a-b=��4��
�ʴ�Ϊm-n����m+n��2-4mn ��m-n��2����m+n��2-4mn=��m-n��2��
���� ���⿼�����д���ʽ���õ���֪ʶ���dz����κ������ε������ʽ���ؼ��Ǹ��������ʽ��ʾ����Ӱ���ֵ������


 �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
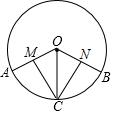 ��ͼ��OA��OB��OC�ǡ�O�İ뾶��$\widehat{AC}$=$\widehat{BC}$��CM��OA��M��CN��OB��N����֤��MC=NC��
��ͼ��OA��OB��OC�ǡ�O�İ뾶��$\widehat{AC}$=$\widehat{BC}$��CM��OA��M��CN��OB��N����֤��MC=NC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com