
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:选择题
| A. | 2cm | B. | 3cm | C. | 小于3cm | D. | 不大于3cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
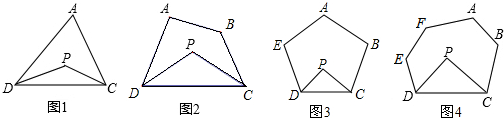
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
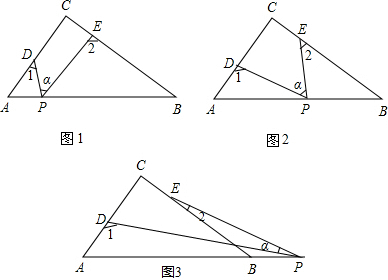
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD是△ABC的高,点Q、M在BC边上,点N在AC边上,点P在AB边上,AD=60cm,BC=40cm,四边形PQMN是矩形.
如图,AD是△ABC的高,点Q、M在BC边上,点N在AC边上,点P在AB边上,AD=60cm,BC=40cm,四边形PQMN是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校为了解 八年级学生课外活动书籍借阅情况,从中随机抽取了50名学生课外书籍借阅情况.将统计结果列出如下的表格,并绘制如图所示的扇形统计图,其中科普类册数占这50名学生借阅总册数的40%.
某校为了解 八年级学生课外活动书籍借阅情况,从中随机抽取了50名学生课外书籍借阅情况.将统计结果列出如下的表格,并绘制如图所示的扇形统计图,其中科普类册数占这50名学生借阅总册数的40%.| 类别 | 科普类 | 教辅类 | 文艺类 | 其他 |
| 册数(本) | 180 | 110 | m | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个三角形各顶点的坐标如图所示,把此三角形先向左平移3个单位长度,再向上平移2个单位长度得到三角形A′B′C′,
一个三角形各顶点的坐标如图所示,把此三角形先向左平移3个单位长度,再向上平移2个单位长度得到三角形A′B′C′,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com