
【题目】点A的坐标为(﹣2,﹣1),点B的坐标为(0,﹣2),若将线段AB平移至A′B′的位置,点A′的坐标为(a,2),点B′的坐标为(1,b),则a+b的值为( )
A. 0 B. 2 C. 4 D. 5
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知CE⊥AB于点E,BD⊥AC于点D,BD与CE交于点O,且AO平分∠BAC.
(1)图中有多少对全等三角形?请你一一列举出来(不要求说明理由).
(2)小明说:欲说明BE=CD,可先说明△AOE≌△AOD得到AE=AD,再说明△ADB≌△AEC得到AB=AC,然后利用等式的性质即可得到BE=CD,请问他的说法正确吗?如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.
(3)要得到BE=CD,你还有其他的思路吗?请仿照小明的说法具体说一说你的想法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级一班在一次活动中要分为四个组,其中第一组有x人,第二组比第一组的![]() 少5人,第三组比一、二组的和少15人,第四组与第一组2倍的和是34.
少5人,第三组比一、二组的和少15人,第四组与第一组2倍的和是34.
(1)用含x的代数式表示第二、三、四组的人数,把答案填在下表相应的位置:
第一组 | 第二组 | 第三组 | 第四组 |
x人 |
|
|
|
x=12 |
|
|
|
(2)求x=12时第二、三、四组的人数,把答案填在上表相应的位置;
(3)求七年级一班的总人数(用含x的代数式表示),并求x=10时,该班的总人数;
(4)x能否等于13,为什么?x能否等于6,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校为搞好新校区的绿化,需要移植树木.该校九年级数学兴趣小组对某棵树木进行测量,此树木在移植时需要留出根部(即CD)1.3米.他们在距离树木5米的E点观测(即CE=5米),测量仪的高度EF=1.2米,测得树顶A的仰角∠BFA=40°,求此树的整体高度AD.(精确到0.1米)(参考数据:sin40°=0.6428,cos40°=0.7660,tan40°=0.8391)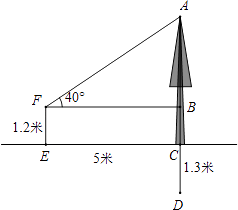
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别是BC、CD上的点,且CE=CF,点P、Q分别是AF、EF的中点,连接PD、PQ、DQ,则△PQD的形状是( )
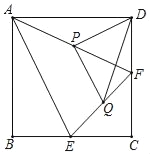
A. 等腰三角形 B. 直角三角形
C. 等腰非直角三角形 D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,在平面直角坐标系中,A、B的坐标分别为(4,0)、(0,3),抛物线y= ![]() x2+bx+c经过点B,且对称轴是直线x=﹣
x2+bx+c经过点B,且对称轴是直线x=﹣ ![]() .
.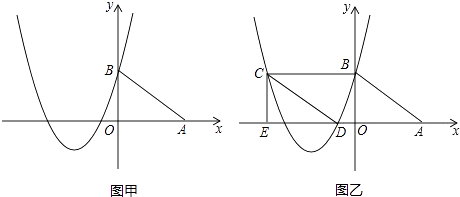
(1)求抛物线对应的函数解析式;
(2)将图甲中△ABO沿x轴向左平移到△DCE(如图乙),当四边形ABCD是菱形时,请说明点C和点D都在该抛物线上;
(3)在(2)中,若点M是抛物线上的一个动点(点M不与点C、D重合),经过点M作MN∥y轴交直线CD于N,设点M的横坐标为t,MN的长度为l,求l与t之间的函数解析式,并求当t为何值时,以M、N、C、E为顶点的四边形是平行四边形.(参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(﹣ ![]() ,
, ![]() ),对称轴是直线x=﹣
),对称轴是直线x=﹣ ![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y= ![]() (x﹣1)2﹣3.
(x﹣1)2﹣3.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com