
【题目】在下列命题中,写出其逆命题,并判断逆命题的真假.
(1)如果两个角相等,那么它们都是对顶角;
(2)直角都相等;
(3)两条平行线被第三条直线所截,所成的同位角相等;
(4)如果![]() ,那么
,那么![]() ;
;
(5)如果一个三角形是直角三角形,那么它的两个锐角互余.
【答案】(1)如果两个角是对顶角,那么它们相等,真命题;(2)如果两个角相等,那么它们都是直角,假命题;(3)同位角相等,两直线平行,真命题;(4)如果![]() ,那么
,那么![]() ,真命题;(5)如果一个三角形的两个内角互余,那么它是直角三角形,真命题.
,真命题;(5)如果一个三角形的两个内角互余,那么它是直角三角形,真命题.
【解析】
分别写出下列定理的逆命题,然后判断真假即可.
(1)如果两个角相等,那么它们都是对顶角的逆命题是如果两个角是对顶角,那么它们相等,为真命题;
(2)直角都相等的逆命题是如果两个角相等,那么它们都是直角,为假命题;
(3)两条平行线被第三条直线所截,所成的同位角相等的逆命题是同位角相等,两直线平行,为真命题;
(4)如果![]() ,那么
,那么![]() 的逆命题是如果
的逆命题是如果![]() ,那么
,那么![]() ,为真命题
,为真命题
(5)如果一个三角形是直角三角形,那么它的两个锐角互余的逆命题是如果一个三角形的两个内角互余,那么它是直角三角形,为真命题.


科目:初中数学 来源: 题型:
【题目】如图,是上海世博园内的一个矩形花园,花园长为100米,宽为50米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为3600米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店某几种型号的计算器每只进价 12 元、售价 20 元,多买优惠, 优惠方法是:凡是一次买 10 只以上的,每多买一只,所买的全部计算器每只就 降价 0.1 元,例如:某人买 18 只计算器,于是每只降价 0.1×(18-10)=0.8(元), 因此所买的 18 只计算器都按每只 19.2 元的价格购买,但是每只计算器的最低售 价为 16 元.
(1)求一次至少购买多少只计算器,才能以最低售价购买? (2)写出该文具店一次销售 x(x>10)只时,所获利润 y(元)与 x(只)之间的函数关系 式,并写出自变量 x 的取值范围;
(3)一天,甲顾客购买了 46 只,乙顾客购买了 50 只,店主发现卖 46 只赚的钱反 而比卖 50 只赚的钱多,请你说明发生这一现象的原因;当 10<x≤50 时,为了 获得最大利润,店家一次应卖多少只?这时的售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 是等边三角形,点E在线段AB上,点D在直线BC上,且
是等边三角形,点E在线段AB上,点D在直线BC上,且![]() ,将
,将![]() 绕点C顺时针旋转
绕点C顺时针旋转![]() 至
至![]() ,连接EF.
,连接EF.
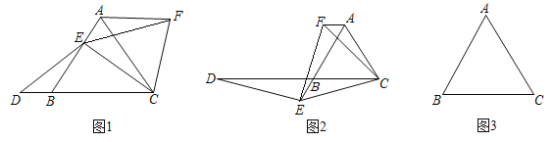
(1)证明:![]() ;
;
(2)如图2,如果点E在线段AB的延长线上,其他条件不变,请你写出线段AB、DB、AF之间的数量关系,并证明你的结论;
(3)如果点E在线段BA的延长线上,其他条件不变,请在图3的基础上将图形补充完整,并写出AB、DB、AF之间的数量关系,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:AB=AD;
(2)求证:CD平分∠ACE.
(3)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】穿楼而过的轻轨、《千与千寻》现实版洪崖洞、空中巴士长江索道……,“3D魔幻城”吸引着海量游客前来重庆打卡.2018年的清明节和“五一”节,洪崖洞入围全球旅游热门目的地榜单,排名仅次于故宫.位于洪崖洞的重庆知名火锅小天鹅火锅在节日期间每天也人满为患,其中鸳鸯火锅和红汤火锅最受游客青睐.在清明节期间,前来就餐选择鸳鸯火锅和红汤火锅的游客共有2200名,鸳鸯火锅和红汤火锅的人均消费分别为130元和120元.
(1)清明节期间,若选择红汤火锅的人数不超过鸳鸯火锅人数的1.5倍.求至少有多少人选择鸳鸯火锅?
(2)“五一”节期间,因天气渐热的原因,前来就餐的游客人数有所下降,与(1)问中选择鸳鸯火锅的人数最少时相比,选择两种火锅的人数均下降了a%;人均消费与清明节期间相比均有所上升,其中鸳鸯火锅的人均消费上涨了a%,红汤火锅的人均消费上涨了![]() %,最终“五一”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
%,最终“五一”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售服装,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,为扩大销售量,减少库存,该商场决定采取适当的降价措施,经调查发现,一件衣服降价
元,为扩大销售量,减少库存,该商场决定采取适当的降价措施,经调查发现,一件衣服降价![]() 元,每天可多售出
元,每天可多售出![]() 件.
件.
![]() 设每件降价
设每件降价![]() 元,每天盈利
元,每天盈利![]() 元,请写出
元,请写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;![]() 若商场每天要盈利
若商场每天要盈利![]() 元,同时尽量减少库存,每件应降价多少元?
元,同时尽量减少库存,每件应降价多少元?
![]() 每件降价多少元时,商场每天盈利达到最大?最大盈利是多少元?
每件降价多少元时,商场每天盈利达到最大?最大盈利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第一个△ABA![]() 中,∠B=20°,AB=A
中,∠B=20°,AB=A![]() B,在A
B,在A![]() B上取一点C,延长AA
B上取一点C,延长AA![]() 到A
到A![]() ,使得A
,使得A![]() A
A![]() =A
=A![]() C,得到第二个△A
C,得到第二个△A![]() A
A![]() C;在A
C;在A![]() C上取一点D,延长A
C上取一点D,延长A![]() A
A![]() 到A
到A![]() ,使得A
,使得A![]() A
A![]() =A
=A![]() D;…,按此做法进行下去,则第5个三角形中,以点A4为顶点的底角的度数为( )
D;…,按此做法进行下去,则第5个三角形中,以点A4为顶点的底角的度数为( )
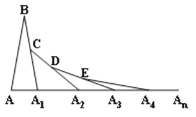
A.5°B.10°C.170°D.175°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com