
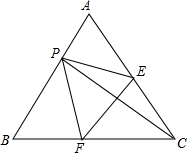
 如图,等边三角形ABC的边长为1,P是AB边上的一个动点(P与A,B不重合),将其折叠点C与点P重合,折痕为EF.
如图,等边三角形ABC的边长为1,P是AB边上的一个动点(P与A,B不重合),将其折叠点C与点P重合,折痕为EF.分析 (1)由∠APE+∠BPF=120°,∠BPF+∠BFP=120°,推出∠APE=∠BFP,即可解决问题.
(2))由△APE∽△BFP,推出$\frac{AP}{BF}$=$\frac{AE}{BP}$=$\frac{PE}{PF}$=$\frac{EC}{CF}$=y,推出AE=y(1-x),BF=$\frac{x}{y}$,推出EC=1-y(1-x),CF=1-$\frac{x}{y}$,再由$\frac{EC}{CF}$=y,列出式子即可解决问题.
解答 (1)证明:∵ △ABC是等边三角形,
△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,
∵点C与点P重合,折痕为EF,
∴∠EPF=∠ECF=60°,
∴∠APE+∠BPF=120°,
∵∠BPF+∠BFP=120°,
∴∠APE=∠BFP,
∴△APE∽△BFP.
(2)解:∵△APE∽△BFP,
∴$\frac{AP}{BF}$=$\frac{AE}{BP}$=$\frac{PE}{PF}$=$\frac{EC}{CF}$=y,
∴AE=y(1-x),BF=$\frac{x}{y}$,
∴EC=1-y(1-x),CF=1-$\frac{x}{y}$,
∵$\frac{EC}{CF}$=y,
∴y=$\frac{1-y(1-x)}{1-\frac{x}{y}}$,
整理得y=$\frac{1+x}{2-x}$,(0<x<1).
点评 本题考查相似三角形的判定和性质、等边三角形的性质、翻折变换等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:选择题
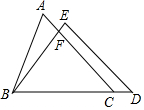 如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE,则∠ACB等于( )
如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE,则∠ACB等于( )| A. | ∠EDB | B. | ∠BED | C. | ∠EBD | D. | ∠ABF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
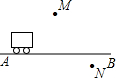 如图,一辆汽车在直线型公路AB上由A向B行驶,M、N分别是位于公路两侧的村庄.
如图,一辆汽车在直线型公路AB上由A向B行驶,M、N分别是位于公路两侧的村庄.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com