
 四点A、C、B、D顺次在一直线上,设AB=a,AC=b,AD=c,并且$\frac{1}{b}$+$\frac{1}{c}$=$\frac{2}{a}$,求证:$\frac{AC}{BC}$=$\frac{AD}{BD}$.
四点A、C、B、D顺次在一直线上,设AB=a,AC=b,AD=c,并且$\frac{1}{b}$+$\frac{1}{c}$=$\frac{2}{a}$,求证:$\frac{AC}{BC}$=$\frac{AD}{BD}$. 分析 首先将$\frac{1}{b}$+$\frac{1}{c}$=$\frac{2}{a}$变形为$\frac{1}{b}$-$\frac{1}{a}$=$\frac{1}{a}$-$\frac{1}{c}$,可得$\frac{a-b}{b}$=$\frac{c-a}{c}$,即$\frac{b}{b-a}$=$\frac{c}{c-a}$,依此即可求解.
解答 证明:∵$\frac{1}{b}$+$\frac{1}{c}$=$\frac{2}{a}$,
∴$\frac{1}{b}$-$\frac{1}{a}$=$\frac{1}{a}$-$\frac{1}{c}$,
$\frac{a-b}{ab}$=$\frac{c-a}{ac}$,
$\frac{a-b}{b}$=$\frac{c-a}{c}$,
∴$\frac{b}{b-a}$=$\frac{c}{c-a}$,
∵$\frac{AC}{BC}$=$\frac{b}{b-a}$,
$\frac{AD}{BD}$=$\frac{c}{c-a}$,
∴$\frac{AC}{BC}$=$\frac{AD}{BD}$.
点评 此题考查了比例线段,关键是将$\frac{1}{b}$+$\frac{1}{c}$=$\frac{2}{a}$变形得到$\frac{b}{b-a}$=$\frac{c}{c-a}$.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
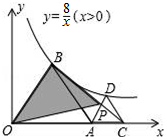 如图,△AOB和△ACD均为正三角形,顶点B、D在双曲线y=$\frac{8}{x}$(x>0)上,线段BC、AD交于点P,则S△OBP=8.
如图,△AOB和△ACD均为正三角形,顶点B、D在双曲线y=$\frac{8}{x}$(x>0)上,线段BC、AD交于点P,则S△OBP=8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
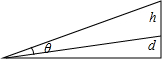 在一个艺术品陈列室内,一幅画的高度为h被悬挂于墙上,其底部边缘距离人的水平视线为d(如图),问人站在离墙多远欣赏这幅画最好?(换句话说怎样使得对应的θ最大)
在一个艺术品陈列室内,一幅画的高度为h被悬挂于墙上,其底部边缘距离人的水平视线为d(如图),问人站在离墙多远欣赏这幅画最好?(换句话说怎样使得对应的θ最大)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com