练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一个的方格图，由粗线隔为个横竖各有个格的“小九宫”格，其中，有一些方格填有至的数字，小鸣在第九行的空格中各填入了一个不大于的正整数，使每行、每列和每个“小九宫”格内的数字都不重复，然后小鸣将第九行的数字从左向右写成一个位数，这个位数是 __________．

    【答案】

    【解析】

    用（7,3）表示位于第7行、第3列的方格，由图形可知，要将3、5、6、7、9填入（9,2）（9,3）（9,6）（9，8）（9,9）中；其中第3、6、8、9列中都含有9，故（9,2）应填9；第3、6、、9列中都含有7，故（9,8）应填7；此题分析规律，试着通过推理就可得到待求的数.

    用（7,3）表示位于第7行、第3列的方格，由图形可知，要将3、5、6、7、9填入（9,2）（9,3）（9,6）（9，8）（9,9）中；

    其中第3、6、8、9列中都含有9，故（9,2）应填9；

    第3、6、、9列中都含有7，故（9,8）应填7；

    第3、6列中都含有3，故（9,3）应填5，（9,6）应填6；

    所以这个9位数应是495186273

    故答案为：495186273

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A=60°，∠D=30°；∠E=∠B=45°）：

    （1）①若∠DCE=40°，则∠ACB的度数为 　．

    ②若∠ACB=128°，则∠DCE的度数为 　．

    （2）由（1）猜想∠ACB与∠DCE的数量关系，并说明理由．

    （3）当∠ACE＜180°且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请直接写出∠ACE角度所有可能的值（不必说明理由）；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校羽毛球队需要购买6支羽毛球拍和盒羽毛球()，羽 毛球拍市场价为150元/支，羽毛球为30元/盒．甲商场优惠方案为：所有商品　九折．乙商场优惠方案为：买1支羽毛球拍送1盒羽毛球，其余原价销售．

    (1)分别用的代数式表示在甲商场和乙商场购买所有物品的费用．

    (2)当时，请通过计算说明选择哪个商场购买比较省钱．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，O是坐标原点。直线y=-x+b经过点A（2，1），AB⊥x轴于B，连结AO。

    （1）求b的值；

    （2）M是直线y=-x+b上异于A的动点，且在第一象限内。过M作x轴的垂线，垂足为N。若△MON的面积与△AOB的面积相等，求点M的坐标。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CD是一高为4米的平台，AB是与CD底部相平的一棵树，在平台顶C点测得树顶A点的仰角α=30°，从平台底部向树的方向水平前进3米到达点E，在点E处测得树顶A点的仰角β=60°，求树高AB（结果保留根号）

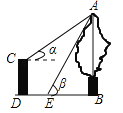
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，四边形ABCD为矩形，，，点E是CD的中点，点P在AB上以每秒2个单位的速度由A向B运动，设运动时间为t秒．

    （1）当点P在线段AB上运动了t秒时，__________________（用代数式表示）;

    （2）t为何值时，四边形PDEB是平行四边形：

    （3）在直线AB上是否存在点Q，使以D、E、Q、P四点为顶点的四边形是菱形？若存在，求出t的值：若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

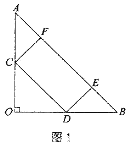
    【题目】在△AOB中，OA=OB=8，∠AOB=90°，矩形CDEF的顶点C、D、F分别在边AO、OB、AB上。

    （1）如图1，若C、D恰好是边AO、OB的中点，则此时矩形CDEF的面积为_________；

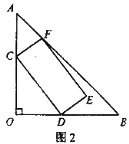
    （2）如图2，若=，求矩形CDEF面积的最大值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数y＝ax2－2ax－1(a是常数,a≠0)，下列结论正确的是( )

    A. 当a＝1时,函数图象过点(－1,1)

    B. 当a＝－2时,函数图象与x轴没有交点

    C. 若a>0,则当x≥1时,y随x的增大而减小

    D. 若a<0,则当x≤1时,y随x的增大而增大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是小明解方程的过程，请你仔细阅读，并解答所提出的问题：

    解：去括号，得

    ． （第一步）

    移项，得

    ． （第二步）

    合并同类项，得

    ． （第三步）

    系数化为1，得

    ． （第四步）

    （1）该同学解答过程从第_____步开始出错，错误原因是______________________；

    （2）写出正确的解答过程．

    查看答案和解析>>

    同步练习册答案