
 如图是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲的体重的取值范围在数轴上表示正确的是( )
如图是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲的体重的取值范围在数轴上表示正确的是( )| A. | 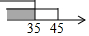 | B. | 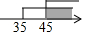 | C. |  | D. |  |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 已知,如图,等腰直角△ABC与等腰直角△CEF,∠ABC=∠CEF=90°,连结AF,M时AF的中点,连结MB,且点C,B,E在同一直线上.求证:BM∥CF.
已知,如图,等腰直角△ABC与等腰直角△CEF,∠ABC=∠CEF=90°,连结AF,M时AF的中点,连结MB,且点C,B,E在同一直线上.求证:BM∥CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 盘秤是一种常见的称量工具,指针转过的角度与被称物体的重量有一定的关系,如下表所示:
盘秤是一种常见的称量工具,指针转过的角度与被称物体的重量有一定的关系,如下表所示:| 重量(单位:千克) | 0 | 1 | 2 | 2.5 | 3 | … | b |
| 指针转过的角度 | 0° | 18° | 36° | a° | 54° | … | 180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
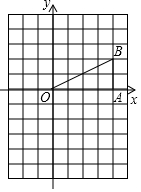 如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
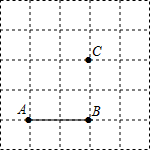 如图,己知线段AB及点C,在方格纸上画图并回答问题.
如图,己知线段AB及点C,在方格纸上画图并回答问题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
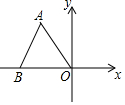 等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )
等边△ABO在平面直角坐标系内的位置如图所示,已知△ABO的边长为6,则点A的坐标为( )| A. | (-3,3) | B. | (3,-3$\sqrt{3}$) | C. | (-3,3$\sqrt{3}$) | D. | (-3,-3$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com