
【题目】如图,∠ADB=∠ACB=90°,AC与BD交于点O,且AC=BD.有下列结论:①AD=BC;②∠DBC=∠CAD;③AO=BO;④AB∥CD.其中正确的是( )

A. ①②③④ B. ①②③ C. ①②④ D. ②③④
【答案】A
【解析】
由已知条件,得到三角形全等,得到结论,对每一个式子进行验证从而确定正确的式子.
∵在Rt△ADB和Rt△BCA中,AB=AB,AC=BD
∴Rt△ADB≌Rt△BCA(HL)
∴AD=BC,∴①正确;
∵∠DAB=∠CBA,∠DBA=∠CAB
∴∠DBC=∠CAD,∴②正确;
在△AOD和△BOC中
∠ADO=∠BCO,∠DOA=∠COB,AD=BC
∴△AOD≌△BOC(AAS)
∴AO=BO,∴③正确;
∵∠CDO+∠DCO+∠COD=180,∠CDO=∠DCO,
∠OAB+∠OBA+∠AOB=180,∠OAB=∠OBA
∠COD=∠AOB
∴∠DCO=∠OAB
∴AB∥CD,∴④正确;
所以以上结论都正确,
故选A.


科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= ![]() (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= ![]() (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 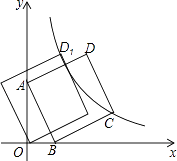
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b(k1≠0)与反比例函数![]() 的图象交于点A(-1,2),B(m,-1).
的图象交于点A(-1,2),B(m,-1).
(1)求一次函数与反比例函数的解析式;
(2)在x轴上是否存在点P(n,0),使△ABP为等腰三角形,请你直接写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.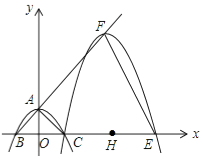
(1)求a,c的值;
(2)连结OF,试判断△OEF是否为等腰三角形,并说明理由;
(3)现将一足够大的三角板的直角顶点Q放在射线AF或射线HF上,一直角边始终过点E,另一直角边与y轴相交于点P,是否存在这样的点Q,使以点P,Q,E为顶点的三角形与△POE全等?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,△AOB为顶点A,B的坐标分别为A(0,4),B(﹣3,0),按要求解答下列问题. 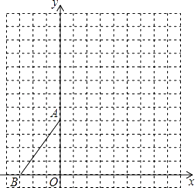
(1)①在图中,先将△AOB向上平移6个单位,再向右平移3个单位,画出平移后的△A1O1B1;(其中点A,O,B的对应点为A1 , O1 , B1)
②在图中,将△A1O1B1绕点O1顺时针旋转90°,画出旋转后的Rt△A2O1B2;(其中点A1 , B1的对应点为A2 , B2)
(2)直接写出点A2 , B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为 . 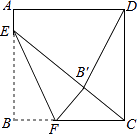
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com