
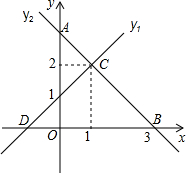
 如图,直线y1与y2相交于点C(1,2),y1与x轴交于点D,与y轴交于点(0,1);y2与x轴交于点B(3,0),与y轴交于点A.下列说法正确的有①②③(直接写序号)
如图,直线y1与y2相交于点C(1,2),y1与x轴交于点D,与y轴交于点(0,1);y2与x轴交于点B(3,0),与y轴交于点A.下列说法正确的有①②③(直接写序号)分析 观察函数图象得到当x>1时,直线y1都在直线y2的上方,于是可对①进行判断;利用待定系数法求出y2的解析式为y=-x+3,则可确定A(0,3),所以OA=OB,于是可对②进行判断;同样可得y1的解析式为y=x+1,易得D(-1,0),则OE=OD,所以∠EDO=45°,于是可对③进行判断;通过计算BD和AB的长可对④进行判断.
解答 解:如图,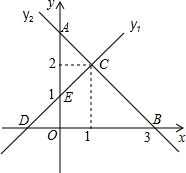
当x>1时,y1>y2,所以①正确;
设y2的解析式为y=kx+b,
把C(1,2),B(3,0)代入得$\left\{\begin{array}{l}{k+b=2}\\{3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
所以y2的解析式为y=-x+3,
当x=0时,y=-x+3=3,则A(0,3),则OA=OB,所以②正确;
同样可得y1的解析式为y=x+1,
当y=0时,x+1=0,解得x=-1,则D(-1,0),
所以OE=OD,则∠EDO=45°,所以③正确;
因为BD=3+1=4,而AB=3$\sqrt{2}$,所以△AOB与△BCD不全等,所以④错误.
故答案为①②③.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.也考查了全等三角形的判定.


科目:初中数学 来源: 题型:解答题
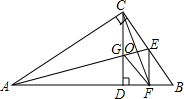 如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC,交BC于点E,CD⊥AB于点D,EF⊥AB于点F,CD交AE于点G,CF交AE于点O.求证:四边形CGFE是菱形.
如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC,交BC于点E,CD⊥AB于点D,EF⊥AB于点F,CD交AE于点G,CF交AE于点O.求证:四边形CGFE是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,AM⊥BD于M,CN⊥BD于N,连接CM、AN
如图,在平行四边形ABCD中,AM⊥BD于M,CN⊥BD于N,连接CM、AN查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com