
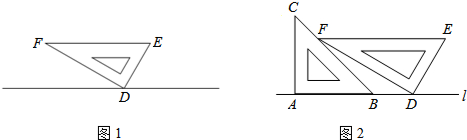
分析 (1)过E作EG⊥l于G,过F作FH⊥l于H,求出∠GED的度数,利用三角函数的知识即可求出EG的长度;
(2)在△FBH和△FHD中,分别求出HB,HD的长度,然后用HD-HB的长度即可求得B、D两点间的距离.
解答 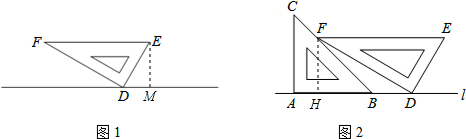 解:(1)过E作EG⊥l于G,
解:(1)过E作EG⊥l于G,
∵∠EFD=30°,∠EDF=90°
∴∠FED=60°,
∴∠GED=30°,
∴GE=$\frac{\sqrt{3}}{2}$DE=5$\sqrt{3}$cm,
∴点E到直线l的距离为5$\sqrt{3}$cm;
(2)∵EF∥AD,
∴FH=EG=5$\sqrt{3}$,
∵∠C=45°,
∴BH=FH=5$\sqrt{3}$,
∵∠FDH=∠EFD=30°,
∴DH=$\sqrt{3}$FH=15,
∴BD=15-5$\sqrt{3}$,即B、D两点间的距离为(15-5$\sqrt{3}$)cm.
点评 本题考查了勾股定理和三角函数的知识,解答本题的关键是根据三角函数的知识在直角三角形中求出直角边的长度,难度适中.


科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD是菱形,E在BC上,F在CD延长线上,AE=BF,AE和BF相交于点G,若tan∠BGE=$\frac{4}{3}$,菱形ABCD的面积为10,则AB的长为$\frac{5\sqrt{2}}{2}$.
如图,四边形ABCD是菱形,E在BC上,F在CD延长线上,AE=BF,AE和BF相交于点G,若tan∠BGE=$\frac{4}{3}$,菱形ABCD的面积为10,则AB的长为$\frac{5\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在边长为20的大正方形中,剪去四个小正方形,可以折成一个无盖的长方体盒子.如果剪去的小正方形边长按整数值依次变化,即分别取1、2、3、…、9、10时,则小正方形边长为3时,所得到的无盖的长方体盒子容积最大.
如图,在边长为20的大正方形中,剪去四个小正方形,可以折成一个无盖的长方体盒子.如果剪去的小正方形边长按整数值依次变化,即分别取1、2、3、…、9、10时,则小正方形边长为3时,所得到的无盖的长方体盒子容积最大.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com