
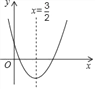
【题目】已知二次函数y=ax2+bx+c的图象如图所示,x=![]() 是该抛物线的对称轴,根据图中所提供的信息,请写出有关a,b,c的四条结论,并简要说明理由.
是该抛物线的对称轴,根据图中所提供的信息,请写出有关a,b,c的四条结论,并简要说明理由.
科目:初中数学 来源: 题型:
【题目】小聪和小明分别从相距30公里的甲、乙两地同时出发相向而行,小聪骑摩托车到达乙地后立即返回甲地,小明骑自行车从乙地直接到达甲地,函数图象y1(km)和y2(km)分别表示小聪离甲地的距离和小明离乙地的距离与已用时间t(h)之间的关系,如图所示.下列说法:①折线段OAB是表示小聪的函数图象y1,线段OC是表示小明的函数图象y2;②小聪去乙地和返回甲地的平均速度相同;③两人在出发80分钟后第一次相遇;④小明骑自行车的平均速度为15km/h,其中不正确的个数为( )
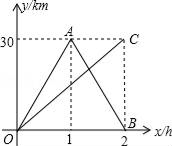
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一方有难八方支援,某市政府筹集抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型可供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)

(1)若全部物资都用甲、乙两种车来运送,需运费8200元,则分别需甲、乙两种车各几辆?
(2)为了节约运费,该市政府共调用16辆甲、乙,丙三种车都参与运送物资,试求出有几种运送方案,哪种方案的运费最省?其费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.
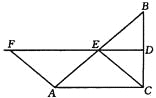
(1)求证:四边形ACEF是平行四边形;
(2)当∠B的大小满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论;
(3)四边形ACEF有可能是正方形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
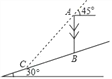
【题目】如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:![]() ≈1.73,
≈1.73,![]() ≈1.41).
≈1.41).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B分别是x轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,3),直线PB交y轴于点D,△AOP的面积为12;
(1)求△COP的面积;
(2)求点A的坐标及p的值;
(3)若△BOP与△DOP的面积相等,求直线BD的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一点,联结
上一点,联结![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
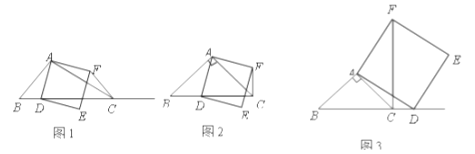
(1)如果![]() ,
,![]() ,
,
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),如图2,线段
不重合),如图2,线段![]() 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段![]() 的数量关系为 ;
的数量关系为 ;
②当点![]() 在线段
在线段![]() 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果![]() ,
,![]() 是锐角,点
是锐角,点![]() 在线段
在线段![]() 上,当
上,当![]() 满足什么条件时,
满足什么条件时,![]() (点
(点![]() 不重合),并说明理由.
不重合),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四个螺丝将四条不可弯曲的本条围成一个木框(形状不限),不记螺丝大小,其中相邻两螺丝之间的距离依次为3,4,5,7.且相邻两本条的夹角均可调整,若调整木条的夹角时不破坏此木框,则任意两个螺丝之间的最大距离是( )
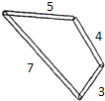
A.6B.7C.8D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
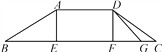
【题目】为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=5![]() 米,tanB=
米,tanB=![]() ,∠C=30°.
,∠C=30°.
(1)求桥面AD与地面BC之间的距离.
(2)因受地形限制,决定对该天桥进行改建,使CD斜面的坡度变陡,将其30°坡角改为40°,改建后斜面为DG,试计算此次改建节省路面宽度CG大约应是多少?(结果精确到0.1米,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com