
 完成以下证明,并在括号内填写理由.
完成以下证明,并在括号内填写理由.分析 根据平行线的判定得出AB∥CE,根据平行线的性质得出∠A=∠4,∠ABC+∠BCE=180°,求出∠3=∠4,根据平行线的判定得出AC∥DE,根据平行线的性质得出∠ACB=∠D,即可得出答案.
解答 证明:∵∠1=∠2,
∴AB∥CE(内错角相等,两直线平行),
∴∠A=∠4(两直线平行,内错角相等),
∠ABC+∠BCE=180°(两直线平行,同旁内角互补),
即∠ABC+∠ACB+∠4=180°,
∵∠A=∠3,
∴∠3=∠4,
∴AC∥DE
∴∠ACB=∠D(两直线平行,同位角相等),
∴∠ABC+∠4+∠D=180°,
故答案为:AB,CE,内错角相等,两直线平行,两直线平行,内错角相等,两直线平行,同旁内角互补,∠4,AC,DE,两直线平行,同位角相等,
点评 本题考查了平行线的性质和判定,能灵活运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:解答题
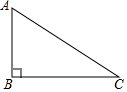 按下列要求画图并填空:
按下列要求画图并填空:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{27}$ | C. | $\sqrt{\frac{3}{2}}$ | D. | $\sqrt{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
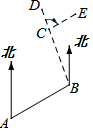 如图,小明从A出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是右转80°.
如图,小明从A出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是右转80°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l1的解析式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
如图,直线l1的解析式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
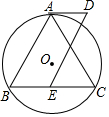 如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,AD是⊙O的切线,点E是BC上一点,且BE=AD.
如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,AD是⊙O的切线,点E是BC上一点,且BE=AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com