
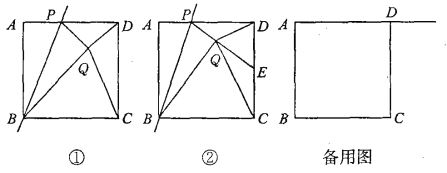
ЎѕМвДїЎїИзНјўЩЈ¬ТСЦЄХэ·ЅРОABCDµД±Яі¤ОЄ1Ј¬µгPКЗAD±ЯЙПµДТ»ёц¶ЇµгЈ¬µгA№ШУЪЦ±ПЯBPµД¶ФіЖµгКЗµгQЈ¬Б¬ЅУPQЎўDQЎўCQЎўBQЈ¬ЙиAPЈЅxЈ®
ЈЁ1Ј©BQЈ«DQµДЧоРЎЦµКЗ_______Ј¬ґЛК±xµДЦµКЗ_______Ј»
ЈЁ2Ј©ИзНјўЪЈ¬ИфPQµДСУі¤ПЯЅ»CD±ЯУЪµгEЈ¬ІўЗТЎПCQDЈЅ90ЎгЈ®
ўЩЗуЦ¤ЈєµгEКЗCDµДЦРµгЈ» ўЪЗуxµДЦµЈ®
ЈЁ3Ј©ИфµгPКЗЙдПЯADЙПµДТ»ёц¶ЇµгЈ¬ЗлЦ±ЅУРґіцµ±ЎчCDQОЄµИСьИэЅЗРОК±xµДЦµЈ®
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј¬
Ј¬![]() ;(2) ўЩАнУЙПкјыЅвОцЈ»ўЪ
;(2) ўЩАнУЙПкјыЅвОцЈ»ўЪ![]() ;(3) 2©Ѓ
;(3) 2©Ѓ![]() »т
»т![]() »т2+
»т2+![]() Ј®
Ј®
ЎѕЅвОцЎї
КФМв·ЦОцЈє(1)ёщѕЭБЅµгЦ®јд,ПЯ¶ОЧо¶МїЙЦЄ,µгQФЪПЯ¶ОBDЙПК±BQЈ«DQµДЦµЧоРЎ,КЗBDµДі¤¶И,АыУГ№ґ№Й¶ЁАнјґїЙЗуіц;ФЩёщѕЭЎчPDQКЗµИСьЦ±ЅЗИэЅЗРОЗуіцxµДЦµ;
(2) ўЩУЙ¶ФіЖїЙЦЄAB=BQ=BC,ТтґЛЎПBCQ=ЎПBQC.ёщѕЭЎПBQE=ЎПBCE=90Ўг,їЙЦЄЎПEQC=ЎПECQ,ґУ¶шEQ=EC.ФЩёщѕЭЎПCQD=90ЎгїЙµГЎПDQE+ЎПCQE=90Ўг, ЎПQCE+ЎПQDE=90Ўг,¶шЎПEQC=ЎПECQ, ЛщТФЎПQDE=ЎПDQEЈ¬ґУ¶шEQ=ED.ТЧµГµгEКЗCDµДЦРµгЈ»ўЪФЪRtЎчPDEЦРЈ¬PE= PQ+QE=x+![]() Ј¬PD=1©ЃxЈ¬PQ=xЈ¬ёщѕЭ№ґ№Й¶ЁАнјґїЙЗуіцxµДЦµ.
Ј¬PD=1©ЃxЈ¬PQ=xЈ¬ёщѕЭ№ґ№Й¶ЁАнјґїЙЗуіцxµДЦµ.
(3) ЎчCDQОЄµИСьИэЅЗРО·ЦБЅЦЦЗйїц:ўЩCDОЄСь,ТФµгC ОЄФІРД,ТФCDµДі¤ОЄ°лѕ¶»»Ў,БЅ»ЎЅ»µгјґОЄК№µГЎчCDQОЄµИСьИэЅЗРОµДQµг; ўЪCDОЄµЧ±ЯК±,ЧчCDµДґ№Ц±ЖЅ·ЦПЯ,Ул![]() µДЅ»µгјґОЄЎчCDQОЄµИСьИэЅЗРОµДQµг,Фт№ІУР 3ёцQµг,ДЗГґТІ№ІУР3ёцPµг,ЧчёЁЦъПЯ,АыУГЦ±ЅЗИэЅЗРОµДРФЦКЗуЦ®јґµГ.
µДЅ»µгјґОЄЎчCDQОЄµИСьИэЅЗРОµДQµг,Фт№ІУР 3ёцQµг,ДЗГґТІ№ІУР3ёцPµг,ЧчёЁЦъПЯ,АыУГЦ±ЅЗИэЅЗРОµДРФЦКЗуЦ®јґµГ.
КФМвЅвОцЈєЈЁ1Ј©![]() Ј¬
Ј¬![]() Ј®
Ј®
ЈЁ2Ј©ўЩЦ¤ГчЈєФЪХэ·ЅРОABCDЦРЈ¬
AB=BCЈ¬ЎПA=ЎПBCD=90ЎгЈ®
ЎЯQµгОЄAµг№ШУЪBPµД¶ФіЖµгЈ¬
ЎаAB=QBЈ¬ЎПA=ЎПPQB=90ЎгЈ¬
ЎаQB=BCЈ¬ЎПBQE=ЎПBCEЈ¬
ЎаЎПBQC=ЎПBCQЈ¬
ЎаЎПEQC=ЎПEQB©ЃЎПCQB=ЎПECB©ЃЎПQCB=ЎПECQЈ¬
ЎаEQ=ECЈ®
ФЪRtЎчQDCЦРЈ¬
ЎЯЎПQDE=90Ўг©ЃЎПQCEЈ¬
ЎПDQE=90Ўг©ЃЎПEQCЈ¬
ЎаЎПQDE=ЎПDQEЈ¬
ЎаEQ=EDЈ¬
ЎаCE=EQ=EDЈ¬јґEОЄCDµДЦРµгЈ®
ўЪЎЯAP=xЈ¬AD=1Ј¬
ЎаPD=1©ЃxЈ¬PQ=xЈ¬CD=1Ј®
ФЪRtЎчDQCЦРЈ¬
ЎЯEОЄCDµДЦРµгЈ¬
ЎаDE=QE=CE=![]() Ј¬
Ј¬
ЎаPE=PQ+QE=x+![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЅвµГ x=![]() Ј®
Ј®
ЈЁ3Ј©ЎчCDQОЄµИСьИэЅЗРОК±xµДЦµОЄ2-![]() Ј¬
Ј¬![]() Ј¬2+
Ј¬2+![]() Ј®
Ј®
ИзНјЈ¬ТФµгBОЄФІРДЈ¬ТФABµДі¤ОЄ°лѕ¶»»ЎЈ¬ТФµгCОЄФІРДЈ¬ТФCDµДі¤ОЄ°лѕ¶»»ЎЈ¬БЅ»Ў·Ц±рЅ»УЪQ1Ј¬Q3Ј®ґЛК±ЎчCDQ1Ј¬Ўч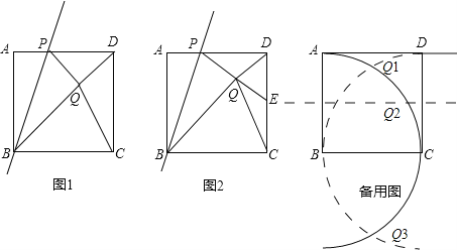
ЎчCDQ2ТФCDОЄµЧµДµИСьИэРОЈ®
ТФПВ¶ФґЛQ1Ј¬Q2Ј¬Q3Ј®·Ц±рМЦВЫёчЧФµДPµгЈ¬ІўЗуAPµДЦµЈ®
МЦВЫQ:ИзНјЧчёЁЦъПЯЈ¬Б¬ЅУBQ1ЎўCQ1Ј¬ЧчPQ1ЎНBQ1Ѕ»ADУЪPЈ¬№эµгQ1Ј¬ЧчEFЎНADУЪEЈ¬Ѕ»BCУЪFЈ®
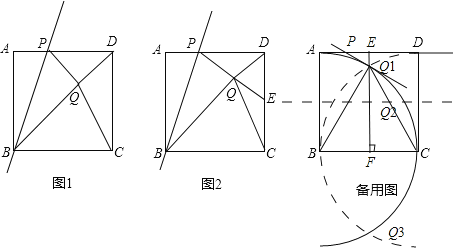
ЎЯЎчBCQ1ОЄµИ±ЯИэЅЗРОЈ¬Хэ·ЅРОABCD±Яі¤ОЄ1Ј¬
Ўа![]() Ј¬
Ј¬![]() Ј®
Ј®
ФЪЛД±ЯРОABPQ1ЦРЈ¬
ЎЯЎПABQ1=30ЎгЈ¬
ЎаЎПAPQ1=150ЎгЈ¬
ЎаЎчPEQ1ОЄє¬30ЎгµДЦ±ЅЗИэЅЗРОЈ¬
ЎаPE=![]() Ј®
Ј®
ЎЯAE=![]() Ј¬
Ј¬
Ўаx=AP=AE-PE=2-![]() Ј®
Ј®
ўЪМЦВЫQ2Ј¬ИзНјЧчёЁЦъПЯЈ¬Б¬ЅУBQ2Ј¬AQ2Ј¬№эµгQ2ЧчPGЎНBQ2Ј¬Ѕ»ADУЪPЈ¬Б¬ЅУBPЈ¬№эµгQ2ЧчEFЎНCDУЪEЈ¬Ѕ»ABУЪFЈ®

ЎЯEFґ№Ц±ЖЅ·ЦCDЈ¬
ЎаEFґ№Ц±ЖЅ·ЦABЈ¬
ЎаAQ2=BQ2Ј®
ЎЯAB=BQ2Ј¬
ЎаЎчABQ2ОЄµИ±ЯИэЅЗРОЈ®
ФЪЛД±ЯРОABQPЦРЈ¬
ЎЯЎПBAD=ЎПBQP=90Ўг, ЎПABQ=60Ўг,
ЎаЎПAPE=120Ўг
ЎаЎПEQ2G=ЎПDPG=180Ўг-120Ўг=60ЎгЈ¬
Ўа![]() Ј¬
Ј¬
ЎаEG=![]() Ј¬
Ј¬
ЎаDG=DE+GE=![]() -1Ј¬
-1Ј¬
ЎаPD=1-![]() Ј¬
Ј¬
Ўаx=AP=1-PD=![]() Ј®
Ј®
ўЫ¶ФQ3Ј¬ИзНјЧчёЁЦъПЯЈ¬Б¬ЅУBQ1Ј¬CQ1Ј¬BQ3Ј¬CQ3Ј¬№эµгQ3ЧчBQ3ЎНPQ3Ј¬Ѕ»ADµДСУі¤ПЯУЪPЈ¬Б¬ЅУBPЈ¬№эµгQ1Ј¬ЧчEFЎНADУЪEЈ¬ґЛК±Q3ФЪEFЙПЈ¬І»·БјЗQ3УлFЦШєПЈ®
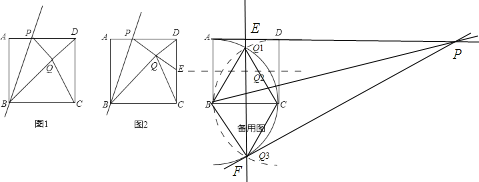
ЎЯЎчBCQ1ОЄµИ±ЯИэЅЗРОЈ¬ЎчBCQ3ОЄµИ±ЯИэЅЗРОЈ¬BC=1Ј¬
Ўа![]() Ј¬
Ј¬![]() Ј¬
Ј¬
Ўа![]() Ј®
Ј®
ФЪЛД±ЯРОABQ3PЦР
ЎЯЎПABF=ЎПABC+ЎПCBQ3=150ЎгЈ¬
ЎаЎПEPF=30ЎгЈ¬
ЎаEP=![]() ,EF=
,EF=![]() Ј®
Ј®
ЎЯAE=![]() Ј¬
Ј¬
Ўаx=AP=AE+PE=![]() +2Ј®
+2Ј®
ЧЫЙПЛщКцЈ¬ЎчCDQОЄµИСьИэЅЗРОК±xµДЦµОЄ2©Ѓ![]() Ј¬
Ј¬![]() Ј¬2+
Ј¬2+![]() Ј®
Ј®


 ГыРЈїОМГПµБРґр°ё
ГыРЈїОМГПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЈЁ2016ЙЅОчКЎЈ©ОТКЎДіЖ»№ы»щµШПъКЫУЕЦКЖ»№ыЈ¬ёГ»щµШ¶ФРиТЄЛН»хЗТ№єВтБїФЪ2000kg©Ѓ5000kgЈЁє¬2000kgєН5000kgЈ©µДїН»§УРБЅЦЦПъКЫ·Ѕ°ёЈЁїН»§Ц»ДЬСЎФсЖдЦРТ»ЦЦ·Ѕ°ёЈ©Јє
·Ѕ°ёAЈєГїЗ§їЛ5.8ФЄЈ¬УЙ»щµШГв·СЛН»хЈ®
·Ѕ°ёBЈєГїЗ§їЛ5ФЄЈ¬їН»§РиЦ§ё¶ФЛ·С2000ФЄЈ®
ЈЁ1Ј©Зл·Ц±рРґіц°ґ·Ѕ°ёAЈ¬·Ѕ°ёB№єВтХвЦЦЖ»№ыµДУ¦ё¶їоyЈЁФЄЈ©Ул№єВтБїxЈЁkgЈ©Ц®јдµДєЇКэ±нґпКЅЈ»
ЈЁ2Ј©Зу№єВтБїxФЪКІГґ·¶О§К±Ј¬СЎУГ·Ѕ°ёA±И·Ѕ°ёBё¶їоЙЩЈ»
ЈЁ3Ј©ДіЛ®№ыЕъ·ўЙМјЖ»®УГ20000ФЄЈ¬СЎУГХвБЅЦЦ·Ѕ°ёЦРµДТ»ЦЦЈ¬№єВтѕЎїЙДЬ¶аµДХвЦЦЖ»№ыЈ¬ЗлЦ±ЅУРґіцЛыУ¦СЎФсДДЦЦ·Ѕ°ёЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЛжЧЕОТ№ъµД·ўХ№УлЗїґуЈ¬ЦР№ъОД»ЇУлКАЅзёч№ъОД»ЇµДЅ»БчУлИЪєПЅшТ»ІЅјУЗїЈ®ОЄБЛФцЅшКАЅзёч№ъИЛГс¶ФЦР№ъУпСФєНОД»ЇµДАнЅвЈ¬ФЪКАЅзёч№ъЅЁБўїЧЧУС§ФєЈ¬НЖ№гєєУпЈ¬ґ«ІҐЦР»ЄОД»ЇЈ®Н¬К±Ј¬ёч№ъѧУ֮јдµДЅ»Бч»о¶ЇТІЦрДкФцјУЈ®ФЪУл№ъјКУСєГѧУЅ»Бч»о¶ЇЦРЈ¬РЎГфґтЛгЦЖЧцТ»ёцХэ·ЅМеАсєРЛНёшНв№ъЕуУСЈ¬ГїёцГжЙП·Ц±рКйРґТ»ЦЦЦР»Єґ«НіГАµВЈ¬Т»№ІУРЎ°ИКТеАсЦЗРЕРўЎ±БщёцЧЦЈ®ИзНјКЗЛэЙијЖµДАсєРЖЅГжХ№їЄНјЈ¬ДЗГґЎ°АсЎ±ЧЦ¶ФГжµДЧЦКЗЈЁЎЎЎЎЈ©
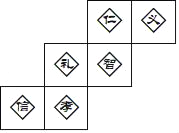
A. ИК B. Те C. ЦЗ D. РЕ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЛД±ЯРОABCDЦРЈ¬AB=CDЈ¬BF=DEЈ¬AEЎНBDЈ¬CFЎНBDЈ¬ґ№Чг·Ц±рОЄEЈ¬FЈ®

ЈЁ1Ј©ЗуЦ¤ЈєЎчABEЎХЎчCDFЈ»
ЈЁ2Ј©ИфACУлBDЅ»УЪµгOЈ¬ЗуЦ¤ЈєAO=COЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ЙдПЯOMЙПУРИэµгAЎўBЎўCЈ¬ВъЧгOA=20cmЈ¬AB=60cmЈ¬BC=10cmЈ¬µгPґУµгOіц·ўЈ¬СШOM·ЅПтТФ1cm/ГлµДЛЩ¶ИФИЛЩФЛ¶ЇЈ¬µгQґУµгCіц·ўФЪПЯ¶ОCOЙППтµгOФИЛЩФЛ¶ЇЈ¬БЅµгН¬К±іц·ўЈ¬µ±µгQФЛ¶ЇµЅµгOК±Ј¬µгPЎўQНЈЦ№ФЛ¶ЇЈ®
ЈЁ1Ј©ИфµгQФЛ¶ЇЛЩ¶ИОЄ2cm/ГлЈ¬ѕ№э¶аі¤К±јдPЎўQБЅµгПаУцЈї
ЈЁ2Ј©µ±PФЪПЯ¶ОABЙПЗТPA=3PBК±Ј¬µгQФЛ¶ЇµЅµДО»ЦГЗЎєГКЗПЯ¶ОABµДИэµИ·ЦµгЈ¬ЗуµгQµДФЛ¶ЇЛЩ¶ИЈ»
![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ЙдПЯOAµД·ЅПтКЗ±±Ж«¶«20ЎгЈ¬ЙдПЯOBµД·ЅПтКЗ±±Ж«Оч40ЎгЈ¬ODКЗOBµД·ґПтСУі¤ПЯЈ®ИфOCКЗЎПAODµДЖЅ·ЦПЯЈ¬ФтЎПBOC=_____ЎгЈ¬ЙдПЯOCµД·ЅПтКЗ_____Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЄБЛМбёЯЙнМеЛШЦКЈ¬УРР©ИЛСЎФсµЅЧЁТµµДЅЎЙнЦРРД¶НБ¶ЙнМеЈ¬ДіЅЎЙнЦРРДµДПы·С·ЅКЅИзПВЈє
Пы·СїЁ | Пы·С·ЅКЅ |
ЖХНЁїЁ | 35ФЄ/ґО |
°ЧЅрїЁ | 280ФЄ/ХЕЈ¬ЖѕїЁГв·СПы·С10ґОФЩЛН2ґО |
ЧкКЇїЁ | 560ФЄ/ХЕЈ¬ЖѕїЁГїґОПы·СІ»ФЩКХ·С |
ТФЙППы·СїЁК№УГДкПЮѕщОЄТ»ДкЈ¬ГїО»№ЛїНЦ»ДЬ№єВтТ»ХЕїЁЈ¬ЗТЦ»ПЮ±ѕИЛК№УГ
ЈЁўсЈ©ИфГїДкИҐёГЅЎЙнЦРРД6ґОЈ¬У¦СЎФсДДЦЦПы·С·ЅКЅёьєПЛгЈї
ЈЁўтЈ©ЙиТ»ДкДЪИҐёГЅЎЙнЦРРДЅЎЙнxґОЈЁxОЄХэХыКэЈ©Ј¬ЛщРиЧЬ·СУГОЄyФЄЈ¬Зл·Ц±рРґіцСЎФсЖХНЁПы·СєН°ЧЅрїЁПы·СµДyУлxµДєЇКэ№ШПµКЅЈ»
ЈЁўуЈ©ИфДіО»№ЛїНГїДкИҐёГЅЎЙнЦРРДЅЎЙнЦБЙЩ18ґОЈ¬ЗлНЁ№эјЖЛг°пЦъХвО»№ЛїНСЎФсЧоєПЛгµДПы·С·ЅКЅЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї°С±Яі¤ОЄ3µДХэ·ЅРОABCDИЖµгAЛіК±ХлРэЧЄ45ЎгµГµЅХэ·ЅРОABЎдCЎдDЎдЈ¬±ЯBCУлDЎдCЎдЅ»УЪµгOЈ¬ФтЛД±ЯРОABODЎдµДЦЬі¤КЗЈЁ Ј©

A. 6![]() B. 6C. 3
B. 6C. 3![]() D. 3+3
D. 3+3![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬Ц±ПЯy=![]() 4x+4УлxЎўyЦб·Ц±рПаЅ»УЪµгAЎўBЈ¬ЛД±ЯРОABCDКЗХэ·ЅРОЈ¬ЕЧОпПЯ
4x+4УлxЎўyЦб·Ц±рПаЅ»УЪµгAЎўBЈ¬ЛД±ЯРОABCDКЗХэ·ЅРОЈ¬ЕЧОпПЯ![]() №эCЈ¬DБЅµгЈ¬ЗТCОЄ¶ҐµгЈ¬ФтaµДЦµОЄ_______.
№эCЈ¬DБЅµгЈ¬ЗТCОЄ¶ҐµгЈ¬ФтaµДЦµОЄ_______.

Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com