
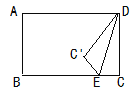
【题目】如图,矩形ABCD中,CD=6,E为BC边上一点,且EC=2将△DEC沿DE折叠,点C落在点C'.若折叠后点A,C',E恰好在同一直线上,则AD的长为( )
A.8B.9C.![]() D.10
D.10
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+m的图象与反比例函数y=![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
(1)求m及k的值;
(2)求点C的坐标,并结合图象写出不等式组0<x+m≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题有两道题,请从(1)、(2)题中选一题作答即可)
(1)某品牌太阳镜由一个镜架和两个镜片配套构成,每个工人每天可以加工![]() 个镜架或者加工
个镜架或者加工![]() 个镜片,现有
个镜片,现有![]() 名工人,应怎么安排人力,才能使每天生产的镜架和镜片配套?能做成多少副太阳镜?
名工人,应怎么安排人力,才能使每天生产的镜架和镜片配套?能做成多少副太阳镜?
(2)去年春季,蔬菜种植场在![]() 公顷的大棚地里分别种植了茄子和西红柿,总费用是
公顷的大棚地里分别种植了茄子和西红柿,总费用是![]() 万元.其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
万元.其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
每公顷费用 万元 | 每公顷获利 万元 | |
茄子 |
|
|
西红柿 |
|
|
请解答下列问题:
①求出茄子和西红柿的种植面积各为多少公顷?
②种植场在这一季共获利多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x+3)(x﹣1)(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=﹣![]() x+b与抛物线的另一个交点为D.
x+b与抛物线的另一个交点为D.
(1)若点D的横坐标为2,求抛物线的函数解析式;
(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;
(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒![]() 个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?

查看答案和解析>>
科目:初中数学 来源: 题型:
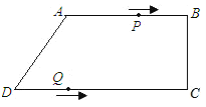
【题目】如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒3cm的速度沿折线A-B-C-D方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动、已知动点P,Q同时出发,当点Q运动到点C时,点P,Q停止运动,设运动时间为t秒,在这个运动过程中,若△BPQ的面积为20cm2 , 则满足条件的t的值有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.![]() B.3 C.1 D.
B.3 C.1 D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.
ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.
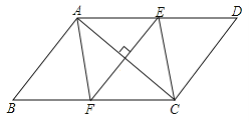
(1)求证:四边形AECF是菱形
(2)若AB=6,BC=10,F为BC中点,求四边形AECF的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
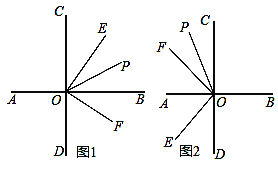
【题目】已知直线CD⊥AB于点O,∠EOF=90°,射线OP平分∠COF.
(1)如图1,∠EOF在直线CD的右侧:
①若∠COE=30°,求∠BOF和∠POE的度数;
②请判断∠POE与∠BOP之间存在怎样的数量关系?并说明理由.
(2)如图2,∠EOF在直线CD的左侧,且点E在点F的下方:
①请直接写出∠POE与∠BOP之间的数量关系;
②请直接写出∠POE与∠DOP之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com