

| ||
| n个6 |
| ||
| (n-1)个6 |
 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
| PA | PB |
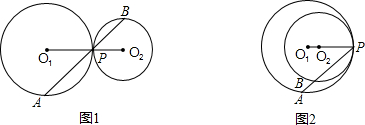 的结论是否成立?为什么?
的结论是否成立?为什么?查看答案和解析>>
科目:初中数学 来源:三维目标导学与测评·数学(北师大版)七年级上册 题型:059
探索题:
已知:如图,点C在线段AB上,线段AC=6cm,BC=4cm,点M,N分别是AC,BC的中点
(1)求:线段MN的长
(2)根据(1)的过程和结果,设AC+BC=a,其他条件不变,你能猜出MN的长吗?为什么?请用一句话表述你发现的规律
查看答案和解析>>
科目:初中数学 来源:期中题 题型:探究题

 =_________.
=_________.查看答案和解析>>
科目:初中数学 来源: 题型:
开放探索题:
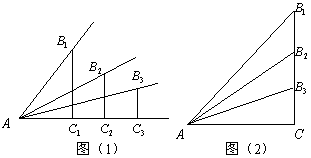
(1)如图,锐角的正弦值和余弦值都随着锐角的确定而确定、变化而变化. 试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律,试比较18°,34°,50°,62°,88°,这些锐角的正弦值和余弦值的大小.
(3)比较大小(在空格处填“>”、“<”或“=”)
若![]() ,则
,则![]() ______
______![]() ;若
;若![]() ,则
,则![]() ______
______![]() ;若
;若![]() >45°,则
>45°,则![]() ______
______![]() .
.
(4)利用互为余角的两个角的正弦和余弦的关系,试比较下列正弦值和余弦值的大小:
Sin10°、cos30°、sin50°、cos70°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com